Geoestatística no R – Lição 28: Ajuste do Variograma Experimetal com geoR

Variograma Experimental no R – Como ajustar usando o geoR

Neste tutorial, vamos ilustrar o ajuste do variograma experimental omnidirecional que já foi ensinado na lição anterior. A biblioteca geoR usa a função variofit, ajuste automático, para a estimativa dos parâmetros do variograma. Posteriormente, também será usada a função lines.variomodel no ajuste do variograma experimental de todas as variáveis ​​numéricas do banco de dados jura.pred.

 

Lines.variomodel

Esta função é um dos métodos utilizados no tutorial para ajustar a variograma experimental. A seguir, há um quadro onde são especificados os argumentos que a função propõe:

cov.model: o modelo do variogram já visto na lição 24.

cov.pars: um vetor concatenado com os valores dos parâmetros da variogrma experimental (patamar, amplitude)

nugget:  Efeito pepita ou Nugget do variograma experimental.

 

 

 

variofit

A função variofit é o nosso segundo método para ajustar o variograma. A seguir, há uma tabela de argumentos válidos para o uso do variofit.

 

fix.nugget: se o valor for estimado, fix.nugget = FALSE; se o valor for fixo, fix.nugget = VERDADEIRO

ini.cov.pars: valores iniciais (patamar, amplitude)

 

 

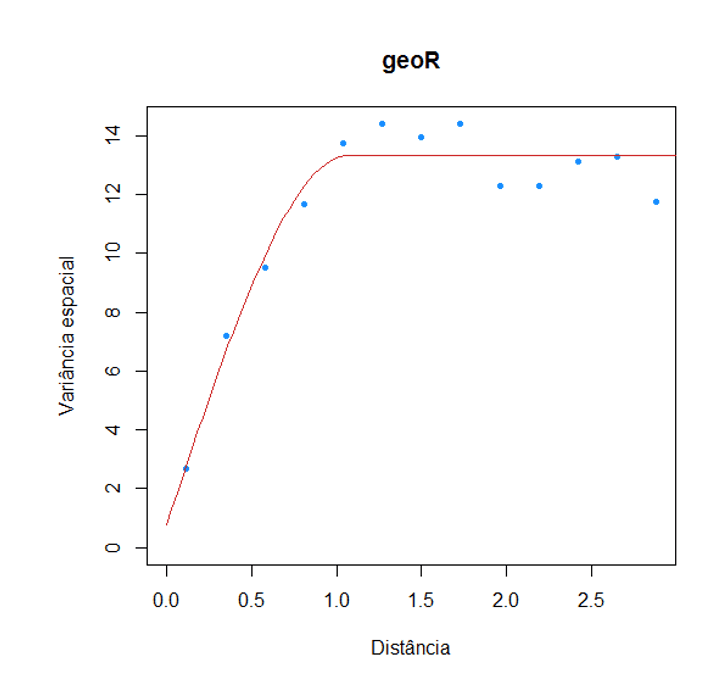
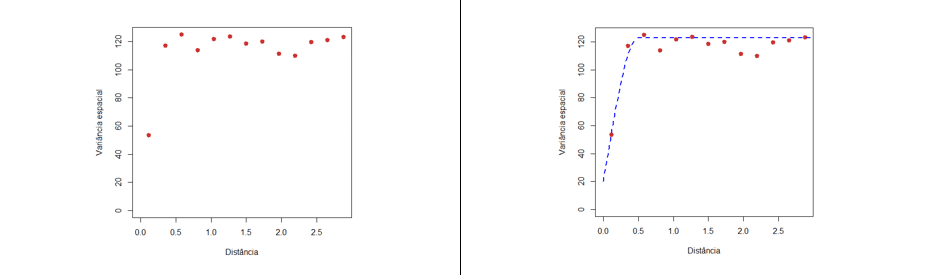
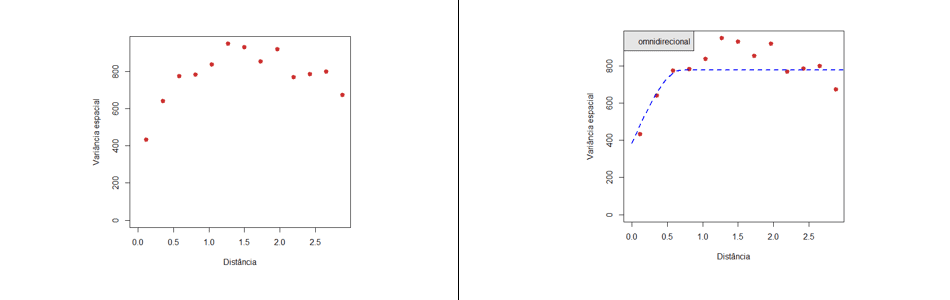
Em seguida observamos o cálculo do variograma experimental das demais variáveis dos dados jura.pred e seu respectivo ajuste. A função que usamos é lines.variomodel. A função variofit será deixada para que o usuário praticar o ajuste do variograma.

 

 

 

 

 

 

 

 

 

 

 

 

 

Aprenda mais sobre Geoestatística com a Geokrigagem:

 

Série de tutoriais: Geoestatística no R – veja a lista

Lição 1 – Como instalar o R

Lição 2 – Objetos e estruturas

Lição 3 – Leitura e gravação de dados

Lição 4 – Estrutura gráfica em R

Lição 5 – Uso dos gráficos no R

Lição 6 – Paleta de cores

Lição 7 – Análises descritivas dos dados

Lição 8 – Distribuições discretas

Lição 9 – Distribuições contínuas

Lição 10 – Regressão linear

Lição 11 – ggplot2 (histograma)

Lição 12 – ggplot2 (boxplot)

Lição 13 – ggplot2 (scatterplot)

Lição 14 – ggplot2 (qq-plot)

Lição 15 – ggplot2 (série temporal)

Lição 16 – ggplot2 (diagrama de área)

Lição 17 – ggplot2 (diagrama circular)

Lição 18 – Pacote sp

Lição 19 – Pacote raster

Lição 20 – Amostragens

Lição 21 – Variograma

Lição 22 – Fenômeno isotrópico

Lição  23 – Modelos teóricos de variogramas

Lição 24 – Fenômeno isotrópico ou anisotrópico?

Lição 25 – Ajuste do variograma experimental com anisotropia

Lição 26 – Ajuste do variograma experimental omnidirecional

Lição 27 – Pacote GeoR

•Lição 28 – Ajuste do variograma experimental com GeoR

Lição 29 – eyefit e vario4 do pacote GeoR

Lição 30 – Design dos dados

Lição 31 – Função gridded

Lição 32 – Validação cruzada

Lição 33 – Krigagem ordinária