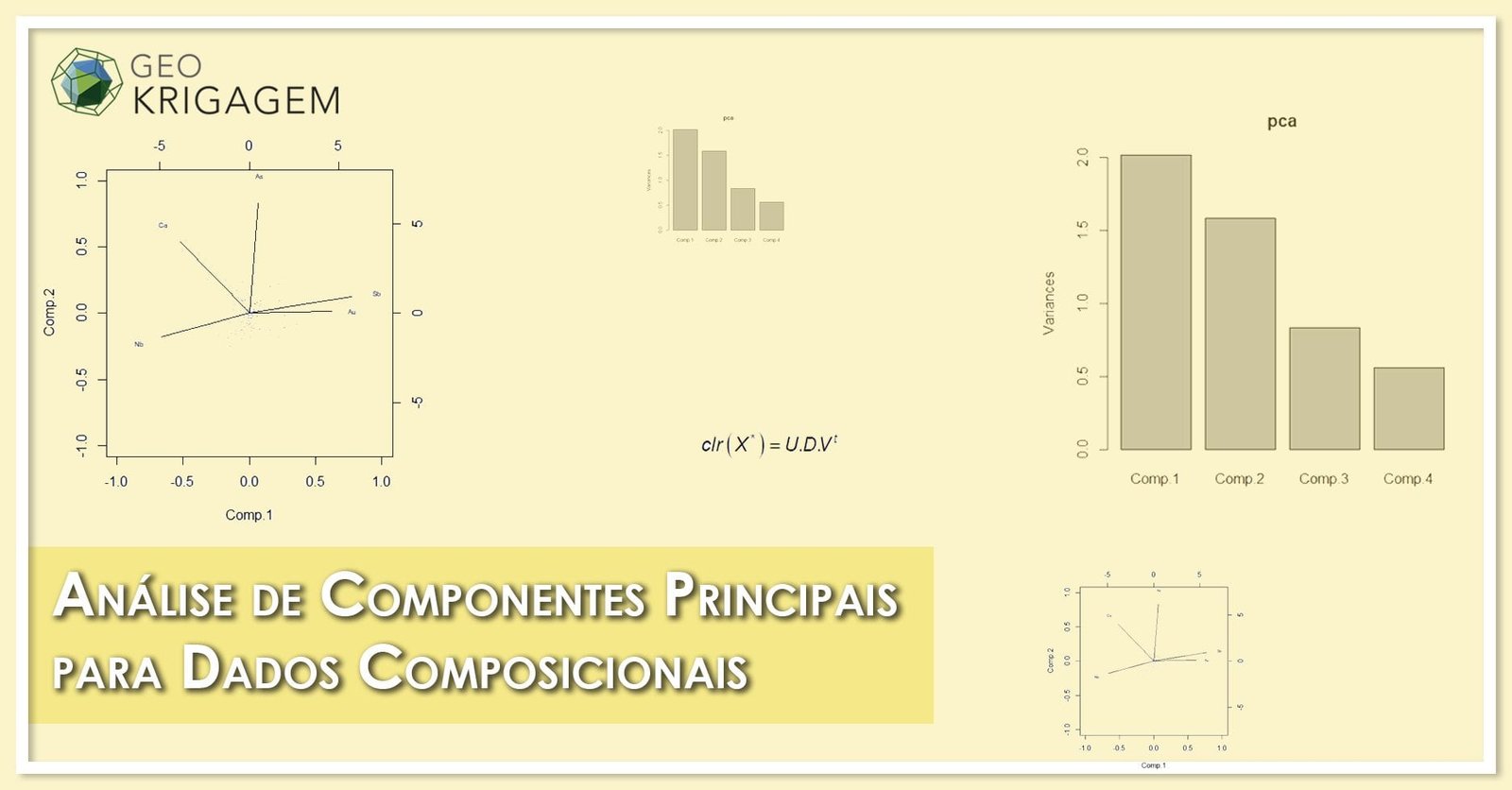
Análise de Componentes Principais para Dados Composicionais
Introdução
Dados composicionais são multivariados por natureza. Para cada técnica de estatística multivariada clássica, há a correspondente versão composicional. PCA, Função Discriminante, Análise de Agrupamento (Cluster), Análise Canônica, etc… têm suas versões composicionais.
Análise de Componentes Principais (PCA)
PCA é uma interpretação de uma decomposição em valores singulares (SVD) de uma matriz de dados. A decomposição SVD é:
Xnp = UnpDppV tpp, no caso de posto completo, isto é, quando todos os elementos da matriz diagonal D forem diferentes de zero.
X é a matriz com n linhas representando n amostras para p atributos ou variáveis
U é uma matriz com colunas ortonormais, denominadas scores
V é uma matriz com colunas ortonormais, denominadas carregamentos (loadings) ou componentes principais
D é uma matriz diagonal cujos elementos são os valores singulares ou autovalores ordenados decrescentemente
Na aplicação não se utilizam todos os elementos na decomposição, mas apenas algumas dimensões, usualmente 2 ou 3. A extensão desse método bastante conhecido na estatística multivariada clássica a dados composicionais é feita aplicando-se a transformação clr ao conjunto inicial de dados. Os carregamentos (loadings) que correspondem às colunas da matriz V e são as componentes principais, as variáveis originais são representadas em termos dessas componentes. Usualmente não se representam todas as componentes.
Loadings:

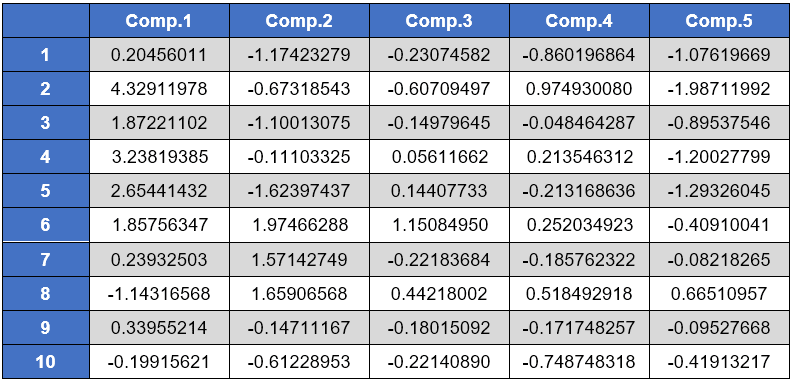
Cada componente adiciona um termo na variância do modelo. No caso com duas componentes o modelo explica 60% da variância e assim por diante.

Um gráfico, denominado screeplot permite visualizar esse ganho progressivo:
Os carregamentos (loadings) que correspondem às colunas da matriz V e são as componentes principais, as variáveis originais são representadas em termos dessas componentes. Usualmente não se representam todas as componentes.
Scores:
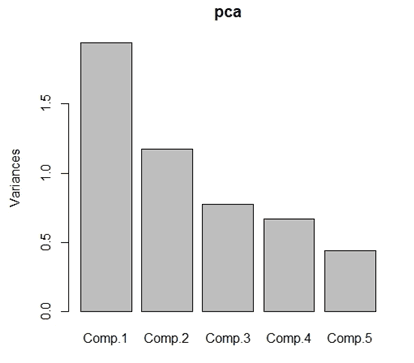
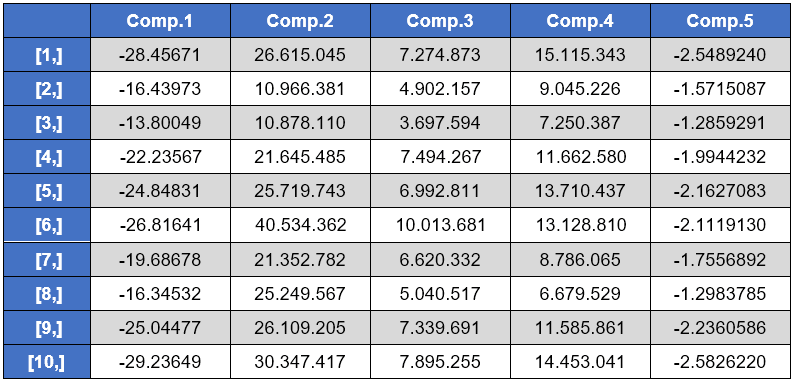
Os scores das dez primeiras amostras em relação às componentes são:
Biplot:
Um gráfico muito empregado na análise exploratória multivariada é o biplot que representa para as duas os três componentes principais tanto os pontos amostrais, como as variáveis.O gráfico biplot pode representar tanto os atributos como as amostras em um gráfico bi ou tridimensional que corresponde às projeções nas duas ou três primeiras componentes.
Na análise clássica o tamanho do vetor é proporcional à variância da variável e o cosseno do ângulo entre dois vetores é a correlação entre as variáveis. Em relação às amostras, pontos próximos podem indicar uma associação entre eles. No caso composicional essa análise muda um pouco.

Análise Componentes Principais Composicional
No caso composicional uma matriz de dados composicionais transformados pelo logaritmo razão centralizada (clr) é decomposta em valores singulares (SVD).
![]()
Loadings:
Os carregamentos (loadings) no caso composicional também devem ser interpretados como composições, não se enumeram todas as componentes que são tantas quantas variáveis a amostra tiver, mas em geral olham-se somente as primeiras.


Analogamente podemos obter o screeplot: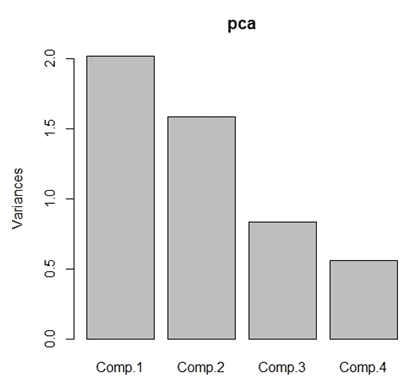
Scores:
Os scores podem ser obtidos com a transformação inversa, representando cada variável em função das componentes o que permite escrever cada linha de X em função das componentes.
Para as dez primeiras amostras os scores correspondentes são:
Biplot:
O gráfico biplot é interpretado de forma diferente. No caso composicional variáveis associadas, e, portanto, com razão próxima de 1, têm as cabeças dos vetores que lhes representam muito próximas. Em contraposição vetores com elevada distância têm comportamento conjunto muito variável. O ângulo entre dois vetores aproxima a correlação entre os logaritmos de suas razões. Pontos próximos têm logaritmos de suas razões semelhantes.
No gráfico a seguir só se vê as duas primeiras componentes.
O biplot composicional da mesma amostra apresentada fica então diferente, revelando um comportamento mais semelhante entre as razões envolvendo as variáveis As e Nb e Sb e Au, enquanto que as variáveis Nb e Ca tem um comportamento diferenciado com respeito ao Au. É importante lembrar que essa área é pobre na mineralização de Au.
O biplot pode ser cotejado com a matriz de variação:
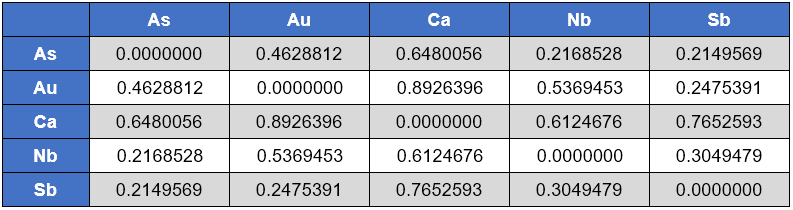
Aonde se vê maior proporcionalidade do Au com Sb e o oposto com o Ca.
Neste texto revisamos os conceitos básicos da análise de componentes principais clássica e apresentamos sua versão composicional. No próximo vamos tratar de dois métodos de agrupamento – dendograma e análise de agrupamento.
Mais artigos sobre “Análise Composicional”
•Introdução à Análise Composicional
•Estatística Descritiva Composicional
Aproveite para aprender mais! O curso online de Análise Composicional do Prof. Dr. Luis Braga tem vagas limitadas.