Estatísticas Descritivas Composicionais
Na abordagem composicional, convertemos os dados em parte de um todo, no pacote compositions* isso é feito pela função acomp que para cada amostra soma os valores em ppm e depois divide cada teor pelo total obtendo um novo componente. Assim uma tabela típica para análise composicional pode ser da forma abaixo:

Definição de dados composicionais
Dados composicionais consistem em vetores cujas componentes são proporções ou porcentagens de algum total. [Leia aqui: “Introdução à Análise Composicional“]
Estatísticas Composicionais
Em particular, a média aritmética e a variância ou desvio padrão dos componentes não se adequam como expressões de tendência central e dispersão. O centro amostral de um conjunto de n valores composicionais (cen) é o fechamento da média geométrica.

Média composicional e razão média
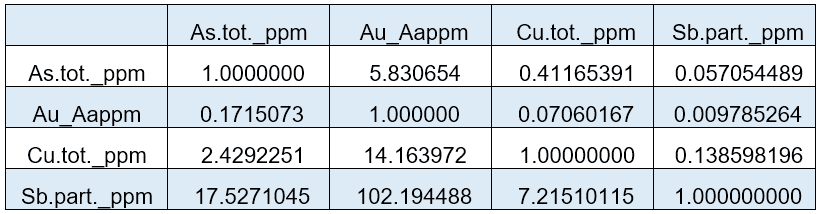
A média composicional para As, Au, Cu e Sb – da amostra apresentada -, é dada na Tabela 1 e a razão média, que é a média geométrica das razões é apresentada na Tabela 2:

Você também pode se interessar por:
Matriz de variação dos elementos
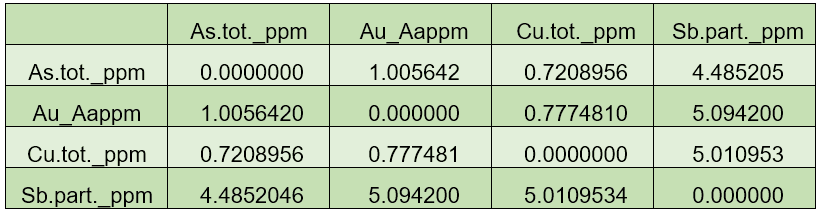
A matriz T de variação descreve a dispersão em um conjunto composicional, o elemento tij é definido como:

Quanto menor o elemento, maior é a proporcionalidade entre os dois componentes, sendo o valor extremo igual a 0 no caso xi=xj . A Tabela 3 apresenta a matriz de variação para quatro elementos: As, Au, Cu e Sb.
Utilizando boxplot
Uma outra forma de explorar a razão entre os componentes é fazer o boxplot das razões entre as composições. No caso das componentes As, Au, Cu e Sb obtem-se o seguinte diagrama que quanto mais centrado em 1 e simétrico, mais proporcionais são as variáveis.

*Pacote desenvolvido por Boogaart e Tolosana utilizado no curso de Análise Composicional da Geokrigagem.
Artigo anterior: “Introdução à Análise Composicional”





