O Espaço Vetorial das Composições
Introdução
Nesta parte, vamos ver como as composições integram uma estrutura de espaço vetorial, base para algumas aplicações importantes, como a estatística multivariada. Embora pareça óbvio, é bom lembrar que, no espaço simplex – que é o espaço das composições -, não contamos mais com as propriedades do espaço euclidiano, então é preciso reinventar a roda.
Você pode se interessar por:
Operações com Composições
Perturbação ou soma
![]()
Um exemplo pode ser encontrado em Boogaart e Tolosana-Delgado (2013) na conversão de proporções de dados nutricionais – gordura, carboidratos e proteínas (g) em proporções de energia(kJ/g). Para uma amostra x com os nutrientes x= [7 10 13] e para um conteúdo energético proporcional de cada componente y= [37 17 17], aplicando-se a operação, obtém-se:
![]()
que são as proporções energéticas de cada componente da amostra.
Potenciação ou Produto por uma constante

A potenciação é um produto externo no sentido que a álgebra linear atribui, portanto, tem as propriedades de associatividade e distributividade.
![]() é um espaço vetorial.
é um espaço vetorial.
Produto Interno (de Aitchinson)

gm é a média geométrica.
Elemento inverso

Subtração
![]()
Norma
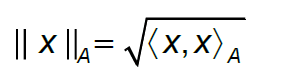
Distância
![]()
Variância generalizada ou total

Matriz de variâncias e covariâncias das composições transformadas clr

Exemplo
No artigo sobre estatísticas descritivas composicionais, apresentamos essa matriz para a amostra considerada.
Uma aplicação das operações de perturbação e potenciação vistas acima é a padronização de dados composicionais via a fórmula seguinte:

Computacionalmente obtemos, para as 10 primeiras amostras, os valores padronizados:






