Variogramas

Variogramas experimentais na Análise Geoestatística

Devido ao interesse demonstrado pelo post anterior vamos explorar um pouco mais o assunto Análise Geoestatística nesta semana, é o caso dos variogramas. Este post corresponde a uma pequena parte da nossa pesquisa desenvolvida ao longo dos anos dedicados à Geoestatística.

A análise geoestatística tem por objetivo determinar o modelo de correlação espacial dos dados. Os métodos geoestatísticos de estimativa e simulação estocástica fazem uso do modelo de correlação espacial, que é o variograma. Os fenômenos espaciais apresentam orientação preferencial (Caers, 2011, p. 82) e, nesse sentido, o variograma deve refletir as características espaciais do fenômeno em estudo. A orientação geológica regional ou local fornece as direções principais para cálculo dos variogramas experimentais. Esse texto será desenvolvido com base no nosso livro texto Geoestatística: conceitos e aplicações (Yamamoto e Landim, 2013, p. 33-53).

Os variogramas experimentais são calculados por meio da função variograma:

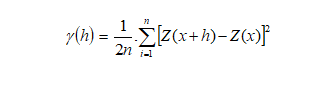
Esta expressão mostra que para uma dada distância h, a função variograma é igual à média das diferenças ao quadrado. Portanto, se trata de uma função da variância espacial. Para calcular um variograma experimental, deve-se definir uma direção e uma distância, para as quais se deseja obter a função variograma. Estes são os dois parâmetros essenciais para o cálculo de um variograma. A direção deve ser compatível com a estrutura geológica da área em estudo. Entretanto, muitas vezes não se sabe a direção do fenômeno espacial subjacente.

Mapa variograma

Nesses casos, deve-se calcular o mapa variograma que permite determinar as direções principais do fenômeno espacial em estudo. Para ilustrar o procedimento da rotina de mapa variograma, vamos considerar a distribuição de uma variável geológica conforme a Figura 1, que mostra uma certa orientação preferencial na direção NW.

Figura 1: Distribuição dos pontos de dados sobre a área de estudo.

Calculando os variogramas

Calculando o mapa variograma (Figura 2), pode-se verificar que existem duas direções 55º e 145º, que correspondem aos eixos de anisotropia do fenômeno espacial. A direção de maior continuidade espacial é 145º e a de menor continuidade a de 55º. Com essa informação, pode-se calcular os variogramas experimentais nestas duas direções (Figura 3).

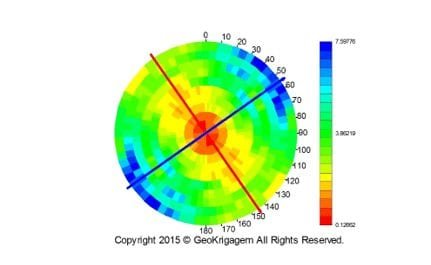
Figura 2: Mapa variograma mostrando as direções de anisotropia do fenômeno espacial.

Figura 3: Variogramas experimentais calculados nas direções de anisotropia.

Como se pode observar na Figura 3, os variogramas tendem a se estabilizar, ou seja, apresentam patamares diferentes. Então, seria interessante definir as propriedades de um variograma típico com patamar (Figura 4).

Figura 4: Propriedades de um variograma típico com patamar.

Essa figura mostra que o variograma tem um patamar em 25, amplitude em 25 e efeito pepita igual a 5. A existência de efeito pepita configura um fenômeno espacial com descontinuidade na origem.

Com esses elementos, pode-se concluir que na Figura 3, a função variograma é diferente para cada uma das direções consideradas. Nestes casos, diz-se que o fenômeno apresenta anisotropia. Com relação aos tipos de anisotropia, pode-se classificar em geométrica (duas amplitudes e um patamar), zonal (uma amplitude e dois patamares) e mista (duas amplitudes e dois patamares), conforme ilustração na Figura 5.

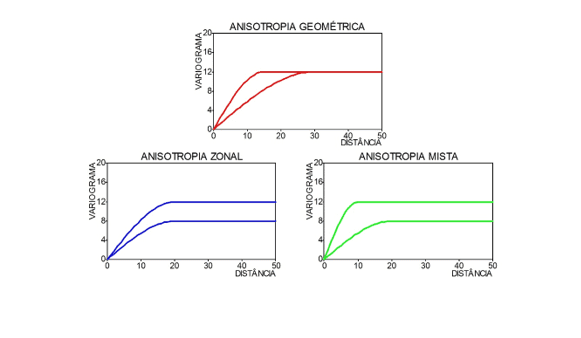Figura 5: Classificação dos tipos de anisotropia de fenômenos espaciais.

O nosso variograma da Figura 3 provavelmente apresenta uma anisotropia mista. O variograma experimental serve para se fazer o ajuste de um modelo teórico, que descreve matematicamente a correlação espacial do fenômeno espacial. Com relação aos modelos teóricos de variogramas, vamos considerar apenas seis, conforme a Figura 6. Estes modelos respondem pela maioria dos casos de variação espacial encontrada na natureza.

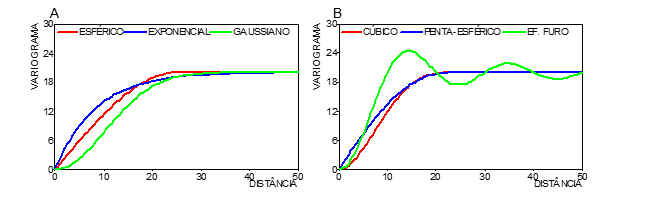
Figura 6: Modelos teóricos de variogramas: A) esférico, exponencial e gaussiano; B)
cúbico, penta-esférico e efeito furo.

Assim, podemos passar ao ajuste de um modelo teórico ao nosso variograma da Figura 3. O ajuste pode ser feito interativamente, por tentativa e erro, pela escolha do modelo teórico, bem como os parâmetros de ajuste: número de estruturas, efeito pepita, variância espacial e amplitude. O resultado desse ajuste se encontra na Figura 7.

Figura 7: Modelo de anisotropia mista ajustado aos variogramas experimentais da Figura 3.

Quer aprender a calcular e modelar variogramas?

Confira aqui nosso curso de Geoestatística: Fundamentos e Aplicações e aprenda muito mais desse universo.

Referências:

Caers, J. 2011. Modeling uncertainty in the Earth Sciences. Sussex, Wiley-Blackwell. 229p.

Yamamoto, J.K.; Landim, P.M.B. 2013. Geoestatística: conceitos e aplicações. São Paulo, Oficina de Textos. 215p.

Este artigo foi útil para você? Compartilhe e conte-nos sobre a sua opinião!