Métodos de interpolação de dados 2D

Nem sempre é possível obter modelos de variogramas representativos, seja pelo caráter aleatório do fenômeno espacial, ou por amostragem insuficiente. Nesses casos, pode-se fazer o mapeamento da distribuição espacial da variável de interesse, por meio dos métodos de interpolação 2D, que são descritos neste capítulo.

Todos os métodos apresentados aqui possuem extensões para dados 3D, mas os exemplos de aplicação e estudos de caso serão feitos apenas para dados 2D. A grande vantagem destes está na possibilidade de se ter uma rápida visualização da distribuição espacial da variável aleatória em estudo.

Além disso, podem ser aplicados para trabalhos de amostragem espacial em progresso, pois os mapas de variação de valores podem revelar regiões que necessitem detalhamentos no plano de amostragem inicial. Esse trabalho de acompanhamento da amostragem é extremamente importante na detecção de anomalias que, muitas vezes, estão associadas à uma mineralização, alvo da exploração mineral.

Geralmente, os métodos de interpolação são aplicados com o objetivo de se obter uma malha regular, em cujos nós os valores da variável de interesse são calculados.

Na verdade, a interpolação de uma malha regular é uma etapa mandatória na análise de dados espaciais, pois mesmo que a amostragem tenha sido planejada em uma malha regular, raramente se obtém as amostras exatamente nas localizações desejadas (Isaaks e Srivastava, 1989, p. 141).

Este artigo reproduz com alguns ajustes a introdução do Capítulo 6 – Métodos de interpolação de dados 2D e o item 6.1.6 – Classificação dos métodos de interpolação do nosso livro Estatística, análise e interpolação de dados geoespaciais.

Classificação dos métodos de interpolação

Os métodos de interpolação podem ser classificados em globais e locais. Os métodos globais ajustam uma única função matemática aos pontos de dados, mas a retirada ou adição de um único ponto de dado irá se propagar sobre o domínio de definição da função. Por outro lado, os métodos locais ajustam funções para pequenas porções da área de estudo, até completar a totalidade da área.

Os métodos globais foram utilizados nas décadas de 1950 e 1960, pois os recursos computacionais eram precários e, portanto, limitados para cálculos complexos e intensivos.

Com relação à precisão da interpolação, os métodos podem ser classificados em exatos e aproximados. Existem funções que se ajustam perfeitamente aos pontos de dados e são chamados de interpoladores exatos e, também, funções que acompanham a tendência geral dos dados, as quais pertencem à classe de interpoladores aproximados.

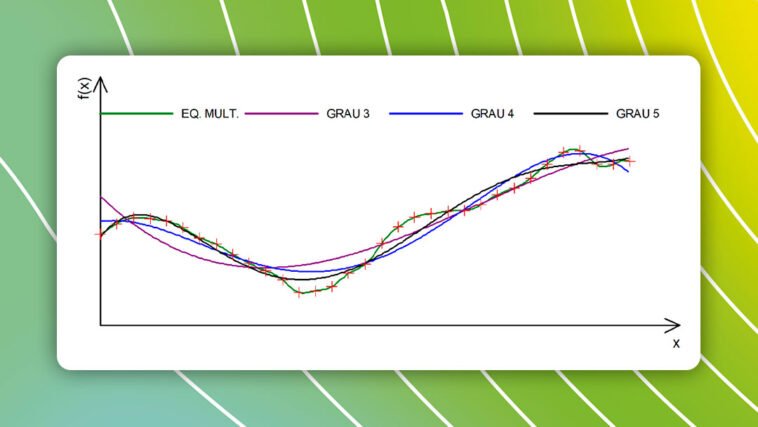
A Figura 1 representa um perfil topográfico, em cujos dados foram ajustadas várias funções matemáticas: equações multiquádricas e polinômios de graus 3 a 5.

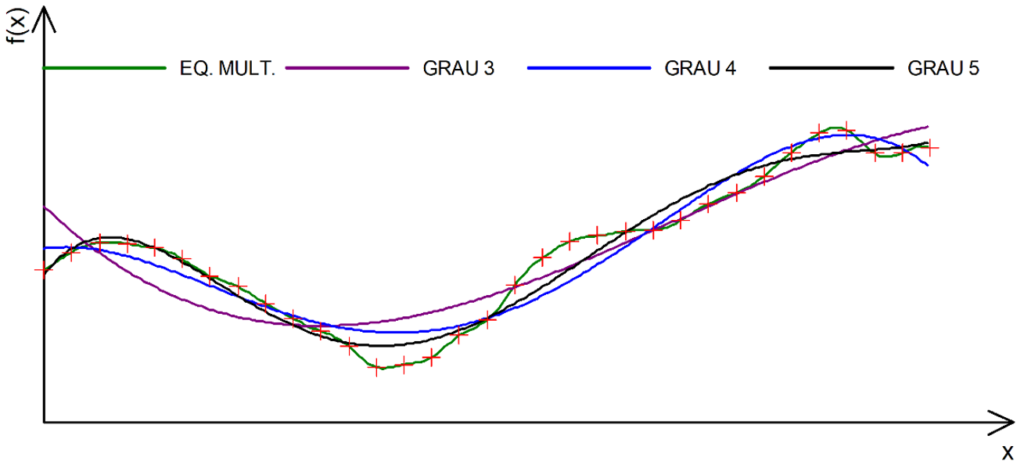
Como se pode observar nesta figura, as equações multiquádricas proporcionam uma interpolação exata, enquanto os polinômios se ajustam conforme a tendência, mas não passam exatamente pelos pontos de dados.

Os métodos de interpolação de dados 2D que estão apresentados neste capítulo encontram-se representados esquematicamente na Figura 2.

Trata-se de métodos usados comumente na prática para a representação da distribuição espacial da variável de interesse. Por esse motivo, estes métodos estão disponíveis em quase todos os programas de computador para análise e representação de dados espaciais.

Conclusão

Referências bibliográficas

Isaaks, E.H.; Srivastava, R.M. 1989, Applied geostatistics, New York, Oxford University Press. 561p.

Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 344p. Incluindo capítulo bônus R na prática com 36p.