Existem dezenas de métodos de interpolação de dados. Alguns são específicos para dados 1D e nem sempre são adaptáveis para dados 2D. Outros métodos necessitam de parâmetros de ajuste que devem ser fornecidos para obtenção de resultados satisfatórios. Assim, o método ideal seria aquele que sejam adaptáveis para dados com dimensões variáveis (1, 2 e 3D) e de preferência com poucos parâmetros de ajuste. Nesse sentido, as equações multiquádricas aparecem como uma excelente opção para interpolação de dados.

Este artigo apresenta a teoria das equações multiquádricas, conforme propostas originalmente por Hardy (1971, p. 1906). A descrição do método será feita com base na interpolação de dados 1D, mas lembrando que as equações multiquádricas são expansíveis para dimensões maiores acrescentando os termos correspondentes. Este artigo reproduz com alguns ajustes o item 6.2.2 Equações multiquádricas do Capítulo 6 – Métodos de interpolação de dados 2D do nosso novo livro Estatística, análise e interpolação de dados geoespaciais (Yamamoto, 2020).
Equações multiquádricas
As equações multiquádricas foram desenvolvidas por Hardy (1971, p. 1906) porque as superfícies de tendência não geravam resultados satisfatórios para fins de engenharia.
Originalmente, as equações multiquádricas foram propostas como um método global de interpolação. Posteriormente, elas foram adaptadas para interpolação local e generalizadas como funções de base radial, sendo o núcleo multiquádrico uma dessas funções. Segundo Franke (1982, p. 191), o método das equações multiquádricas é o mais impressionante em termos de capacidade de ajuste e suavidade visual. Desenvolve-se este item como um método global, que dá excelentes resultados, em termos de continuidade, suavidade e exatidão da superfície gerada.
A forma geral da equação multiquádrica em 2D, segundo Hardy (1971, p. 1906):
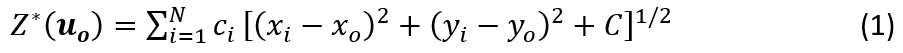
Onde os coeficientes são determinados pela resolução de um sistema de equações lineares (Hardy, 1971, p. 1907):

Em forma matricial, tem-se:

Onde

C é uma constante positiva e, segundo Franke (1982, p. 191), o método é bastante estável com relação à essa constante dando, consistentemente, bons resultados.
Como se pode verificar, o sistema de equações lineares (2) tem a dimensão igual ao número de pontos de dados (N). Certamente, esse é um fator limitante desse método para um grande número de pontos de dados.
Os métodos diretos de resolução de sistemas lineares permitem trabalhar com dimensões iguais a 500 ou mais equações, mas o problema não está no tamanho e no tempo de processamento, mas na propagação de erros por truncamento e arredondamento. Sendo assim, é prudente limitar a aplicação das equações multiquádricas globais para até 500 pontos de dados.
Além disso, outra consideração muito importante é o tamanho do sistema, pois quanto maior a matriz dos coeficientes, maior o número de condição (Kansa, 1990, p. 132). Quando o número de condição da matriz é infinito, a matriz é singular; se for um valor muito grande, então a matriz é mal condicionada (Press et al., 1989, p. 63).
A grande vantagem da proposta multiquádrica está justamente na extensão ou restrição da equação (1), pelo aumento ou redução da dimensionalidade do problema. Para interpolação de dados em um perfil (1D), a equação (1) pode ser reescrita como:

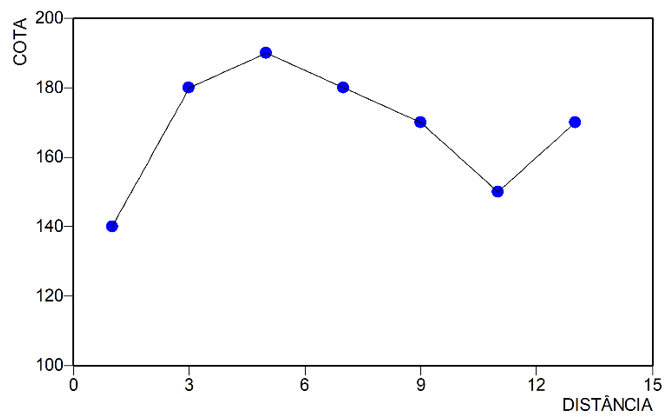
O perfil topográfico da Figura 1 foi interpolado com uma equação multiquádrica 1D da forma da equação (3).
Para dados 3D, basta acrescentar a coordenada z, como segue:

Esta equação foi aplicada para fazer a interpolação de dados de sondagens (3D) para obtenção dos modelos representados no início deste artigo.
Procedimento passo a passo para interpolação multiquádrica
Como um exemplo numérico do processo de cálculo dos coeficientes multiquádricos, considere-se os dados de elevação de terreno medidos em um perfil a pontos regularmente distribuídos (Tabela 1).

Para interpolação dos dados da Tabela 1, utiliza-se o interpolador conforme a equação (3), cujos coeficientes são encontrados pela solução do sistema de equações lineares:

Considerando a constante C igual a zero, tem-se o sistema de equações lineares:

Observe-se que os elementos da diagonal principal são compostos pela raiz quadrada da constante C. Os coeficientes calculados do sistema de equações estão listados na Tabela 2. Esses coeficientes são então aplicados na equação (3) para interpolação do perfil topográfico entre os pontos amostrados (Figura 1).
Observe-se que os pontos amostrais foram unidos por segmentos de reta, ou seja, uma interpolação linear. Isto se deve ao uso da constante nula na equação (3). Para demonstrar o efeito da constante C, a Figura 2 apresenta o resultado da interpolação multiquádrica com duas constantes maiores que zero.
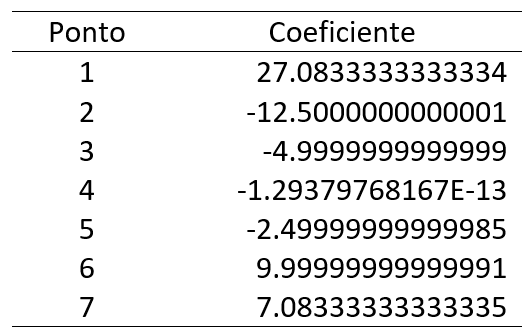

Os coeficientes calculados para essas constantes estão apresentados na Tabela 3.

Os coeficientes são muito diferentes não apenas nos valores absolutos, mas também nos sinais que podem estar invertidos. A Figura 2 mostra o efeito da constante C na interpolação multiquádrica. Uma pequena constante, no caso igual a 1, é suficiente para produzir uma suavização deixando a curva resultante suave e contínua, além de honrar os pontos amostrais.
Entretanto, uma constante muito grande (C=50) pode produzir efeitos indesejados, por exemplo, o deslocamento do mínimo dado pelo ponto 6 (distância=11) para uma distância em torno de 12.
O significado geométrico de cada termo da equação (3) pode ser observado na Figura 4, na qual os termos quádricos estão representados individualmente, sendo que a interpolação multiquádrica resultante é igual à soma deles. Os termos quádricos estão orientados conforme os sinais dos coeficientes (Tabelas 2 e 3).
Nessa figura, pode-se verificar a diferença entre a constante nula e a constante maior que zero. Quando a constante é nula, cada forma quádrica é representada por uma função de valor absoluto, enquanto para constantes maiores que zero, a forma quádrica é uma hipérbole (Hardy, 1977, p. 477). Além disso, quanto maior a constante maior o achatamento da forma quádrica.

Exemplo de aplicação com dados 2D
Para ilustrar uma aplicação da interpolação com dados 2D, apresenta-se na Figura 4 os resultados da interpolação com dados de topografia de Davis (1986, p. 313-314).

Como se pode verificar, as diferenças entre as constantes utilizadas são pequenas, neste exemplo. Salienta-se que a constante quando muito alta pode provocar uma excessiva suavização dos valores interpolados.
Considerações finais
Este artigo descreveu o método das equações multiquádricas para interpolação de dados em 1D, 2D ou 3D. Evidentemente, a metodologia envolvida permite a extensão para dimensões maiores, bastando para isso acrescentar o termo correspondente à nova dimensão. Trata-se de um método de interpolação de aplicação geral, de formulação simples e com resultados bastante satisfatórios.
Incentivamos o Leitor a reproduzir os resultados obtidos com os dados da Tabela 1. Se estiver interessado em verificar como os métodos de interpolação podem ser usados na interpolação de dados 2D, o Leitor poderá consultar o Capítulo 6 – Métodos de interpolação de dados 2D (Yamamoto, 2020, p. 142-183).
Referências bibliográficas
Franke, R. 1982. Scattered data interpolation: test of some methods. Math. of Computation. V. 38, p. 181-200.
Hardy, R.L. 1971. Multiquadric equations of topography and other irregular surfaces. J. Geophysical Research, V. 76, p. 1905-1915.
Hardy, R.L. 1977. Least square prediction. Photogrammetric Engineering and Remote Sensing. V. 43, p. 475-492.
Kansa, E.J. 1990. Multiquadrics – a scattered data approximation scheme with applications to computational fluiddynamics – I. Comput. Math. Applic., v. 19. P. 127-145.
Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. 1989. Numerical recipes in Pascal. New York, Cambridge University Press. 759p.
Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 344p. Incluindo capítulo bônus R na prática com 36p.




