A questão do empilhamento de dados nos variogramas experimentais
Os principais métodos geoestatísticos de estimativa e simulação são baseados no modelo de correlação espacial descrito pela função variograma. Muitas vezes, os variogramas se apresentam com grandes flutuações, devido ao pequeno número de pares de pontos. Neste artigo, de variogramas experimentais, vamos mostrar como o empilhamento de dados pode diminuir tais flutuações e, dessa forma, facilitar o ajuste de um modelo teórico de variograma.
Calculando o variograma
O variograma é calculado por meio da função variograma, descrita pela seguinte expressão:

Para cada distância h (direção e distância), procura-se os pares de pontos que estejam dentro dessa distância e assim suas diferenças ao quadrado são acumuladas na somatória. Ao final, a somatória é dividida pelo número de pares de pontos, que é uma variância média para uma determinada distância h. Evidentemente, essa variância média está sujeita à flutuação estatística, principalmente quando o número de pares de pontos é pequeno.
Para essa demonstração, vamos considerar os dados de espessura da camada de carvão de Sapopema (PR) utilizados por Yamamoto e Landim (2013, p. 38), conforme o mapa de localização das sondagens da Figura 1.
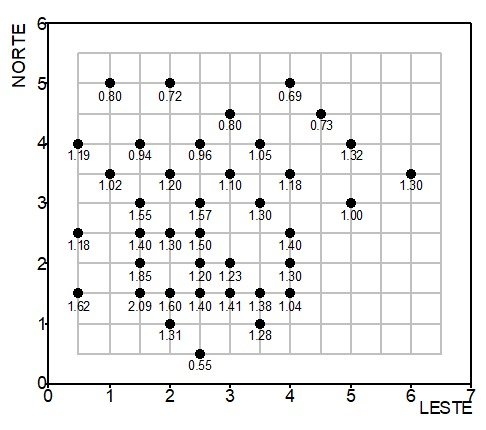
da camada de carvão (Yamamoto e Landim, 2013, p. 37).

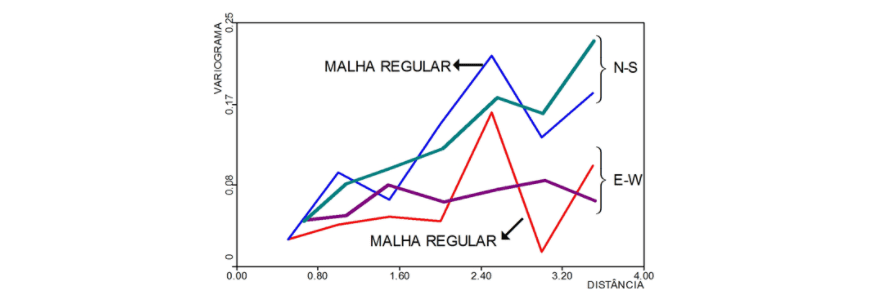
Leste-Oeste (90º), calculados diretamente da malha regular.
Como se pode verificar nesta figura, os dados estão em uma malha regular, onde muitas sondagens não foram executadas. Assim, pode-se calcular o variograma nas direções Leste-Oeste e Norte-Sul usando a disposição regular dos pontos de dados, onde os pares de pontos são obtidos diretamente nas suas posições originais. O resultado desse cálculo pode ser visto na Figura 2, onde se destaca o pequeno número de pares de pontos.
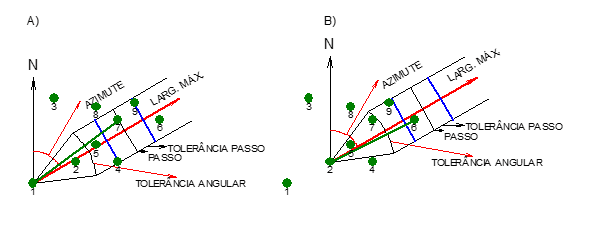
Por outro lado, pode-se aplicar um dispositivo de pesquisa de pontos como se os dados estivessem com distribuição irregular. Este dispositivo (Figura 3) é centrado em cada ponto de dado, a partir do qual se desenha um cone definido pela direção e tolerância angular, bem como pelo passo, tolerância do passo e largura máxima. Para os dados em questão, os parâmetros utilizados encontram-se na Tabela 1.

Fazendo isso, obtém-se os variogramas experimentais apresentados na Figura 4, onde o número de pares de pontos aumentou consideravelmente em relação ao inicial. Esses variogramas ainda mostram algumas flutuações, mas muito menos que aquelas representadas na Figura 2.
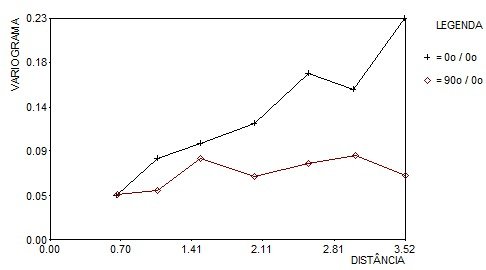
calculados com base no procedimento de busca de dados irregulares.
O empilhamento de dados
Representando-se os dois cálculos em um único gráfico (Figura 5), pode-se verificar que o empilhamento de dados diminui significativamente as flutuações estatísticas, tornando mais fácil o processo de ajuste do modelo teórico de variograma. Além disso, este é um processo que permite extrair a melhor informação dos dados.

pesquisa para dados com distribuição irregular (traço grosso).
Referências
Yamamoto, J.K.; Landim, P.M.B. 2013. Geoestatística: conceitos e aplicações. São Paulo, Oficina de Textos. 215p.