Geoestatística Para Avaliação de Recursos Minerais (Goovaerts, 1997)
Original: “Geostatistics for Natural Resources Evaluation”

Em 1997, Pierre Goovaerts publica uma extensiva revisão apresentada em seu livro intitulado “Geoestatística para avaliação de recursos minerais”, cujo prefácio, escrito por André Journel, tem o seguinte trecho:
“como uma última observação, cuidado com a incerteza… que surge do nosso conhecimento impreciso do fenômeno, que é dependente dos dados e mais importante dependente do modelo, que representa o fenômeno. Nenhum modelo, consequentemente nenhuma medida de incerteza por ser objetiva.”
Além disso, André Journel adjetiva a variância de krigagem como ilusória. Segundo Journel (Goovaerts, 1997, p. VIII), o futuro da geoestatística está na modelagem da incerteza localmente em cada nó por meio de simulações condicionais e globalmente por imagens estocásticas.
Capítulos
Esse livro está apresentado em nove capítulos:
- Introdução;
- Análise exploratória de dados;
- Modelo de função aleatória;
- Inferência e modelagem;
- Estimativa local para um simples atributo;
- Estimativa local: considerando informação secundária;
- Avaliação da incerteza local;
- Avaliação da incerteza espacial;
- Sumário.
Capítulo 1 – uso de dados Jura
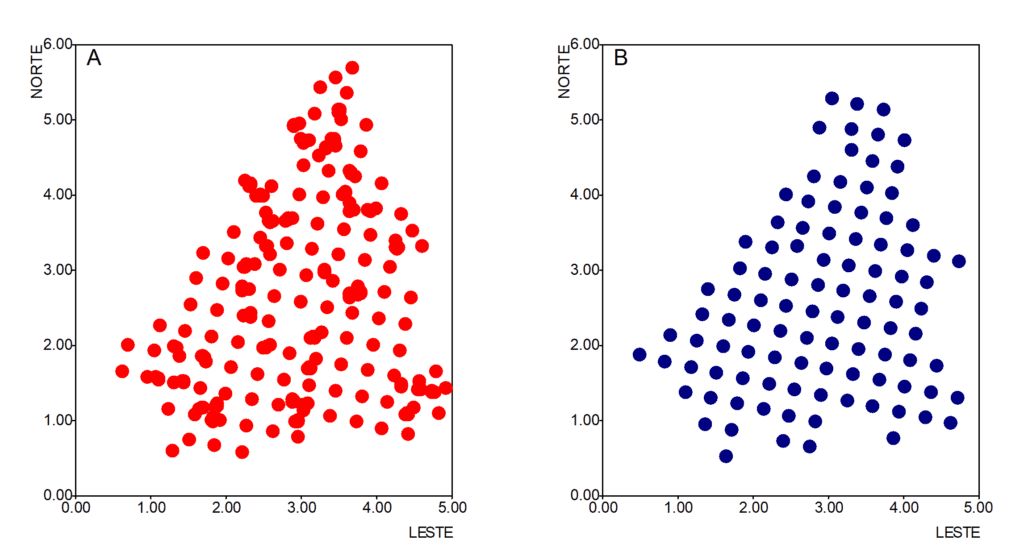
No Capítulo 1, Goovaerts (1997, p.4-6) apresenta um conjunto de dados denominado Jura composto por 359 pontos de dados, nos quais foram medidas as concentrações de sete metais pesados (cádmio, cobalto, crômio, cobre, níquel, chumbo e zinco), bem como duas variáveis categóricas: uso do solo e tipo de rocha. Os dados desse conjunto foram subdivididos em um conjunto denominado predição (259 pontos de dados, figura 1A) e um outro chamado validação (100 pontos de dados, figura 1B).
Esses dados têm sido intensivamente utilizados por diversos trabalhos acadêmicos e, nesse sentido, serão empregados neste livro para ilustrar os procedimentos geoestatísticos expostos.
Capítulo 2
Descrição univariada
A análise exploratória de dados, no Capítulo 2, faz a descrição univariada dos dados de Jura, os quais incluem duas variáveis categóricas (uso do solo e tipo da rocha) e variáveis contínuas. Goovaerts (1997, p. 10) mostra a codificação indicadora para variáveis categóricas, que permite trabalhar matematicamente com elas, ou seja, cálculo de variogramas experimentais e estimativas por meio da krigagem indicadora.
Descrição bivariada
Na descrição bivariada, o autor aborda o diagrama de dispersão, medidas da relação bivariada, descrição univariada espacial e a descrição bivariada espacial. Goovaerts (1997, p. 26-229) apresenta as medidas de continuidade e variabilidade: função covariância, correlograma e semivariograma. Além disso, trata especificamente dessas medidas para as variáveis indicadoras: função covariância indicadora e correlograma indicadora.
Capítulo 3 – The random function model
O Capítulo 3 é intitulado “Modelo de função aleatória”, onde o autor apresenta os modelos determinístico e probabilístico. Segundo Goovaerts (1997, p. 60), o modelo determinístico atribui a uma localização não amostrada um valor z*(u) para um valor desconhecido z(u), sem considerar o erro potencial z*(u)-z(u). Por outro lado, o modelo probabilístico proporciona um conjunto de valores possíveis juntamente com as probabilidades de ocorrência para uma localização não amostrada z(u), ou seja, a distribuição de z dentro da área de estudo (Goovaerts, 1997, p. 60-61). Goovaerts (1997, p. 66-67) ilustra duas distribuições extremas: A) sem incerteza e B) máxima incerteza (Figura 2).

Capítulo 4
O assunto da inferência e modelagem são tratados no Capítulo 4. Na verdade, segundo Goovaerts (1997, p. 75), após a escolha do modelo de função aleatória, trata-se em inferir os dois primeiros momentos da função aleatória Z(u), que são necessários para a krigagem.
Para inferência das estatísticas globais, há necessidade de evitar os problemas associados ao agrupamento dos pontos de dados. São apresentados os métodos de desagrupamento: método poligonal e por células. A seguir são apresentados e discutidos os modelos de correlação espacial por meio tanto do variograma como da função covariância.
Capítulo 5
No Capítulo 5, o autor descreve a estimativa local considerando apenas um atributo. São apresentados todos os modelos associados à krigagem ordinária: krigagem simples e da média.
Além disso, trata da questão da krigagem na presença de tendência, bem como a krigagem fatorial (Goovaerts, 1997, p. 139-168). Goovaerts (1997, p. 179) caracteriza a variância de krigagem como: dependente do modelo de covariância, dependente da configuração dos dados e independente dos valores dos dados.
Capítulo 6
No Capítulo 6, o autor apresenta a questão da estimativa local, considerando a informação secundária, seja ela categórica ou contínua, por meio da cokrigagem. Segundo Goovaerts (1997, p. 217), a influência dos dados secundários na cokrigagem depende: da correlação entre as variáveis primária e secundária; padrão da continuidade espacial dos atributos; configuração espacial das localizações dos dados primários e secundários e densidade de amostragem de cada variável.
Capítulo 7
A avaliação da incerteza local é exposta no Capítulo 7, onde o autor apresenta as aproximações multiGaussiana e indicadora para derivação da função de distribuição acumulada condicional. A função de distribuição acumulada condicional pode ser aplicada para determinar a probabilidade que a probabilidade da variável aleatória é menor ou igual a um determinado valor (Goovaerts, 1997, p. 331);
![]()
A variância condicional pode ser calculada analiticamente como (Goovaerts, 1997, p. 336):
![]()
Na prática, essa integral é aproximada por uma soma discreta (Goovaerts, 1997, p. 336):
![]()
Onde é o valor médio da classe (zk-1, zk), ou seja, e a média condicional igual a (Goovaerts, 1997, p. 337):
![]()
Referência
GOOVAERTS, P. Geostatistics for Natural Resources Evaluation. Nova Iorque. Oxford University Press. 1997. 483p.
Resenhas anteriores:
Retrospectiva da Geoestatística XII: GSLIB (Deutsch e Journel, 1992)
Retrospectiva da Geoestatística XI: Glossário da Geoestatística e Dicionário Multi-idiomas (Olea, 1991)
Retrospectiva da Geoestatística X: Uma Introdução à Geoestatística Aplicada (Isaaks e Srivastava, 1989)
Leia a primeira resenha da série:
Retrospectiva da Geoestatística I: Tratado de Geoestatística Aplicada (Matheron)






