Retrospectiva da Geoestatística X: Uma Introdução à Geoestatística Aplicada (Isaaks e Srivastava, 1989)
Uma década depois do livro de Clark (1979) “Geoestatística Prática” (leia a resenha aqui), Isaaks e Srivastava (1989) publicam “Uma Introdução à Geoestatística Aplicada” (“ An Introduction to Applied Geostatistics “), que apresenta a teoria conforme o formalismo original.
Divisão de capítulos
Este livro está dividido em 21 capítulos:
- Introdução;
- Descrição univariada;
- Descrição bivariada;
- Descrição espacial;
- O conjunto de dados completos;
- O conjunto amostral;
- Continuidade espacial: dados amostrais;
- Estimativa;
- Modelos de função aleatória;
- Estimativa global;
- Estimativa pontual;
- Krigagem ordinária;
- Krigagem de bloco;
- Estratégia de pesquisa;
- Validação cruzada;
- Modelando o variograma amostral;
- Cokrigagem;
- Estimando uma distribuição;
- Mudança de suporte;
- Avaliando a incerteza;
- Considerações finais.
Capítulo 1
No Capítulo 1, Isaaks e Srivastava disponibilizam uma base de dados, denominada “Lago Walker” em Nevada nos Estados Unidos.
Esta base de dados foi derivada de um modelo de elevação digital de terreno com 78.000 pontos, sobre uma malha retangular de 260 por 300 nós, composta por três variáveis, sendo duas contínuas e uma discreta (Isaaks e Srivastava, 1989, p. 4).
Esta base denominada completa serviu para extração de uma amostra com 470 pontos de dados (Figura 1), que foi usada para:
- descrição de feições importantes dos dados;
- estimativa de um valor médio sobre uma área grande;
- estimativa de um valor desconhecido em uma localização particular;
- estimativa de um valor médio sobre pequenas áreas; verificar a performance de uma metodologia de estimativa;
- melhorar a estimativa de uma variável baseada em outra;
- estimativa da distribuição de uma variável sobre uma grande área e também pequenas áreas; estimativa da distribuição das médias de blocos e
- quantificar a incerteza associada às estimativas.

Capítulos 2, 3 e 4
Os Capítulos 2 e 3 apresentam os conceitos estatísticos para dados uni e bivariados.
O Capítulo 4 trata da questão da descrição espacial, onde Isaaks e Srivastava (1989, p. 52-55) os introduzem o diagrama de dispersão h, que se destina à verificação da correlação entre os dados separados por uma distância h: Z(x) contra Z(x+h). O momento de inércia, que é a própria função variograma para uma distância h, pode ser calculada como (Isaaks e Srivastava, 1989, p. 56):
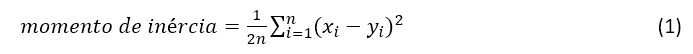
Capítulos 5 e 6
Os Capítulos 5 e 6 analisam os dados completos e amostrais, onde os autores descrevem estatisticamente as populações e suas amostras (Isaaks e Srivastava, 1989, p. 67-139).
Capítulos 7 e 8
O Capítulo 7 descreve a continuidade espacial dos dados amostrais. Com relação aos variogramas experimentais, cabe uma observação que o cálculo de um variograma omnidirecional não implica que a continuidade espacial é a mesma em todas as direções, mas serve meramente como ponto de partida para a definição da distância para que produza uma clara estrutura (Isaaks e Srivastava, 1989, p. 144). Outro destaque é a pesquisa dos eixos de anisotropia por meio do mapa variograma (Isaaks e Srivastava, 1989, p. 149-154).
No Capítulo 8, os autores tratam da questão da estimativa, que tem a finalidade de predizer valores em áreas não amostradas. Os métodos de estimativa fazem uso da equação geral da combinação linear ponderada (Isaaks e Srivastava, 1989, p. 185):

Onde v1, v2, …, vn são os n dados disponíveis e w1, w2, …, wn são os pesos atribuídos a esses dados. Conforme estes autores, esta expressão também pode ser adaptada para fazer a estimativa de dados transformados:

Onde T(v) é a função de transformação.
Capítulo 9
O Capítulo 9 descreve os modelos de função aleatória, onde os autores introduzem o conceito de variáveis aleatórias. O valor esperado de uma variável aleatória pode ser calculado como uma média ponderada pela probabilidade de ocorrência (Isaaks e Srivastava, 1989, p. 208):

Segundo Isaaks e Srivastava (1989, p. 209), se a lei de probabilidade é conhecida, a variância da variável aleatória pode ser calculada como:

Capítulos 10 e 11
O Capítulo 10 aborda a questão da estimativa global e, nesse sentido, são apresentados os métodos de desagrupamento dos dados (desagrupamento poligonal e por células), onde os autores aventam a possibilidade de se empregar os pesos da krigagem ordinária para fazer o desagrupamento (Isaaks e Srivastava, 1989, p. 247-248).
No Capítulo 11, os autores discutem os métodos de estimativa pontual, onde são apresentados os métodos determinísticos: poligonal (vizinho mais próximo), triangulação e inverso da distância. Cabe ressaltar a observação que um método perfeito de estimativa daria um resultado que sempre combina com o valor real, onde o diagrama de dispersão entre esses valores seria uma linha reta e o julgamento da qualidade poderia ser o quão próximo está a dispersão dos valores (Isaaks e Srivastava, 1989, p. 260).
Capítulos 12 e 13
O Capítulo 12 é dedicado ao assunto da krigagem ordinária, que detalha todo o desenvolvimento para se chegar ao sistema de equações de krigagem, que parte da variância do erro envolvendo a variância de uma média ponderada (Isaaks e Srivastava, 1989, p. 283). A solução do sistema de equações de krigagem leva em consideração dois aspectos importantes: distância e agrupamento:

A krigagem de bloco é apresentada no Capítulo 13. Segundo Isaaks e Srivastava (1989, p. 323), a krigagem de bloco é feita a partir da discretização a área local em muitos pontos e então calcular a média das estimativas individuais.
Capítulos 14 e 15
A estratégia de pesquisa é uma etapa importante na krigagem, conforme o Capítulo 14. É importante saber a distância média para dados distribuídos irregularmente, conforme a seguinte equação (Isaaks e Srivastava, 1989, p. 341):

A validação cruzada é uma ferramenta geoestatística de grande importância e é tratada no Capítulo 15. Esta técnica, segundo Isaaks e Srivastava (1989, p. 351), permite fazer a comparação entre valores estimados e reais, com base somente a informação disponível dos pontos de dados. Ainda segundo estes autores, os resíduos derivados da validação cruzada fornecem importante informação espacial, pois podem indicar regiões com problemas de estimativa.
Capítulos 16 e 17
O Capítulo 16 trata da modelagem de variogramas amostrais, onde os autores apresentam a teoria e fazem a modelagem dos dados amostrais do Lago Walker.
A cokrigagem é apresentada no Capítulo 17, especificamente os autores descrevem a cokrigagem ordinária. Cabe uma observação em que a cokrigagem ordinária com duas condições de restrição produz resultados pouco satisfatórios (Isaaks e Srivastava, 1989, p. 415).
Capítulos 18 e 19
A estimativa de uma distribuição é o foco do Capítulo 18. Seja global ou local, pode ser feita com as ferramentas descritas nos capítulos anteriores. Assim, para a distribuição global, deve-se considerar a aplicação do desagrupamento, enquanto para a distribuição local, além do desagrupamento, avalia-se também a distância, conforme a equação (1), segundo Isaaks e Srivastava (1989, p. 417).
Além disso, o capítulo contempla a krigagem indicadora, que é a técnica indicada para a estimativa de distribuição local em pontos não amostrados.
O Capítulo 19 se refere à mudança de suporte, onde se mostra importante relação que mostra a mudança de suporte, por meio da variância de dispersão (Isaaks e Srivastava, 1989, p. 479):

Capítulos 20 e 21
Segundo esses autores, essa expressão mostra que a variância dos pontos dentro de uma certa área pode ser vista como a variância dos valores dos pontos dentro dos blocos mais a variância dos blocos.
No Capítulo 20, os autores tratam da questão da avaliação da incerteza, com abordagem pelo intervalo de confiança e pela distribuição de probabilidade.
Finalmente, o Capítulo 21 traz uma discussão sobre a correta aplicação das diferentes ferramentas e suas limitações.

Referência:
Isaaks, E.H.; Srivastava R. M. 1989. An Introduction to Applied Geostatistics. Nova Iorque, Oxford University Press. 561p.
Veja a série Retrospectiva da Geoestatística:
Retrospectiva da Geoestatística VIII: Geoestatística Prática, por Isobel Clark (1979)
O GKY, programa desenvolvido pelo Prof. Dr. Jorge Kazuo Yamamoto, é uma ótima ferramenta para compatibilizar dados de diferentes campanhas de sondagens. Baixe a versão demo gratuitamente clicando aqui:






