Geoestatística

Matheron (1971, p. 5) definiu geoestatística como a aplicação da Teoria das Variáveis Regionalizadas para a estimação de depósitos minerais, com todas as suas implicações. Assim, tem início a geoestatística na mineração na década de 1970. Os primeiros livros sobre o tema surgem em 1977 e 1978: Geostatistical ore reserve estimation (M. David) e Mining geostatistics (A.G. Journel e C.J. Huijbregts).

Michel David obtém os títulos de mestrado (1969) e doutorado (1973) na Escola Politécnica em Montreal e se torna professor assistente mesmo antes de completar o seu doutorado. Andre Journel assume o cargo de professor assistente na Universidade Stanford em 1978. Journel idealiza o SCRF – Stanford Center for Reservoir Forecasting, voltado para aplicações de geoestatística para a indústria do petróleo. Dessa forma, tem-se início à divulgação da geoestatística e, consequentemente, aplicação em outras áreas do conhecimento.

Neste artigo, vamos apresentar as ferramentas básicas da geoestatística: variograma e krigagem, que atendem aos dois objetivos principais da Teoria das Variáveis Regionalizadas, segundo Matheron (1971, p. 5). A partir disso, pode-se passar para outras técnicas, tais como krigagem não linear e simulação estocástica, que dependem do variograma.

Variograma

A função variograma é empregada para descrever o modelo de correlação espacial da variável de interesse, ou seja, segundo Matheron (1971), expressar as propriedades estruturais do fenômeno espacial. Os fenômenos espaciais apresentam orientação preferencial (Caers, 2011, p. 82) e, nesse sentido, o variograma deve refletir as características  espaciais do fenômeno em estudo.

No caso de dados geológicos, a orientação geológica regional ou local fornece as direções principais para o cálculo dos variogramas experimentais. Entretanto, quando não se tem essa informação a priori, pode-se calcular o mapa variograma que fornece as direções principais do fenômeno espacial em estudo.

Para se calcular a função variograma, aplica-se a seguinte expressão (Yamamoto, 2020, p. 106):

Onde, Z(x) representa uma variável aleatória conforme o vetor de coordenadas (x), h é a distância de separação entre dois pontos e n é o número de pares de pontos separados por h.

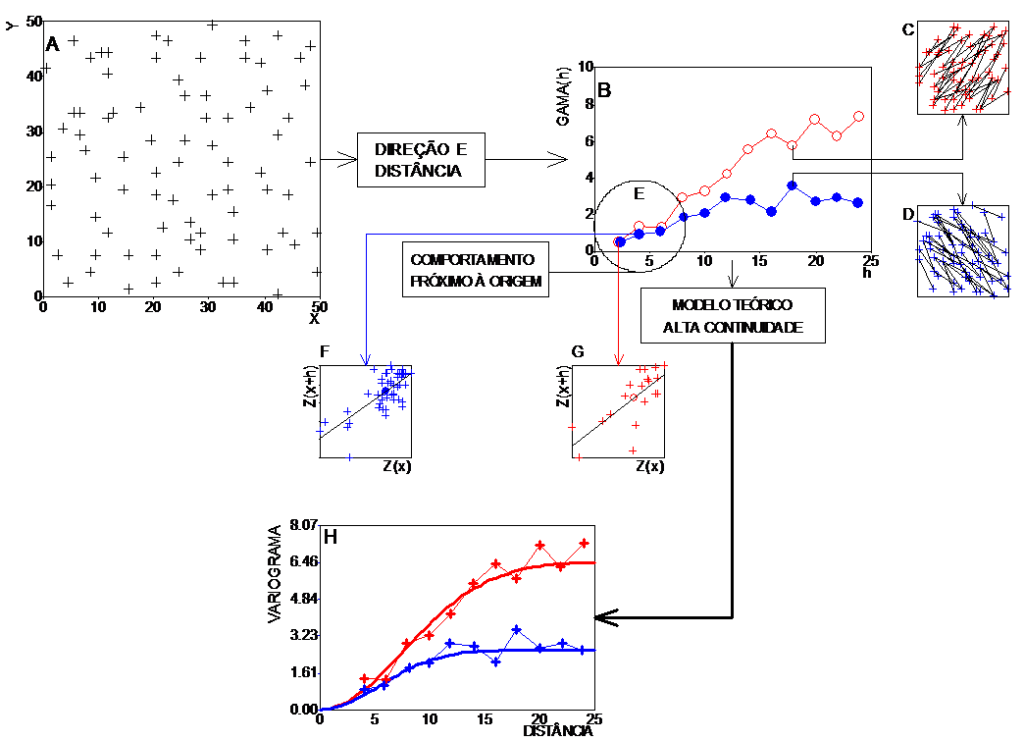
A função variograma depende apenas de dois parâmetros: distância e direção (Figura 1). Cada ponto do variograma representa uma correlação de Z(x+h) contra Z(x) (Figuras 1F e 1G). No exemplo dessa figura, as duas direções principais são 45 e 135^o, como se pode verificar nos vetores formados pelos pares de pontos (Figuras 1C e 1D). A partir dos variogramas experimentais (Figura 1B), ajusta-se o modelo teórico que descreve a correlação espacial (Figura 1H). Deve-se ressaltar que a distribuição dos pontos de dados (Figura 1A) tem um papel importante no cálculo de variogramas experimentais.

Para ilustração do processo de cálculo de variogramas experimentais, vamos considerar os pontos de dados de teores simulados de CaO, conforme o mapa de localização da Figura 2. Sabe-se que a estrutura geológica regional é N135. Mas, supondo-se que não se tem conhecimento a priori desta informação, vamos construir o mapa variograma que permite definir as direções preferenciais do fenômeno espacial (Figura 3).

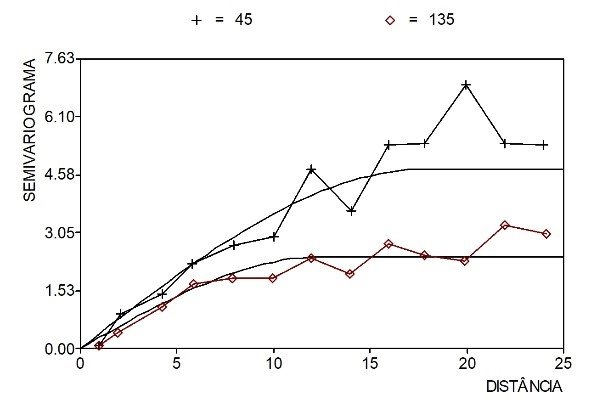
O mapa variograma mostra claramente as duas direções principais: N45 e N135. Define-se como direção de maior continuidade aquela que apresenta menor patamar e, portanto, se trata da direção N135. Com base nesta informação, passa-se ao cálculo dos variogramas experimentais nas duas direções principais e ajuste do modelo de correlação espacial (Figura 4).

Como se pode verificar, trata-se de um modelo com anisotropia zonal. Detalhes da correção da anisotropia zonal ou mista podem ser vistos em Yamamoto (2020, p. 133-136).

Krigagem

Agora, podemos estimar a distribuição espacial da variável de interesse (teores simulados de CaO). O estimador da krigagem ordinária é baseado na fórmula da média ponderada (Yamamoto, 2020, p. 193):

Onde λ_i, i=1,n são os pesos da krigagem ordinária associados aos n pontos de dados e x_o é o centro da célula da malha regular.  

Para proceder à krigagem ordinária, define-se uma malha regular, onde se calcula os teores nos centros das células (Yamamoto 2020, p. 143). Nem todos os pontos da malha regular poderão ser calculados, pois se saírem do domínio amostral os resultados refletem uma extrapolação matemática, o que não nos interessa.

Assim, trabalha-se com o conceito da fronteira convexa que é o polígono convexo de área mínima que engloba os pontos de dados (Yamamoto, 2020, p. 144). Feito isso, passa-se à estimativa da malha regular por meio da krigagem ordinária, de acordo com os resultados apresentados na Figura 5.

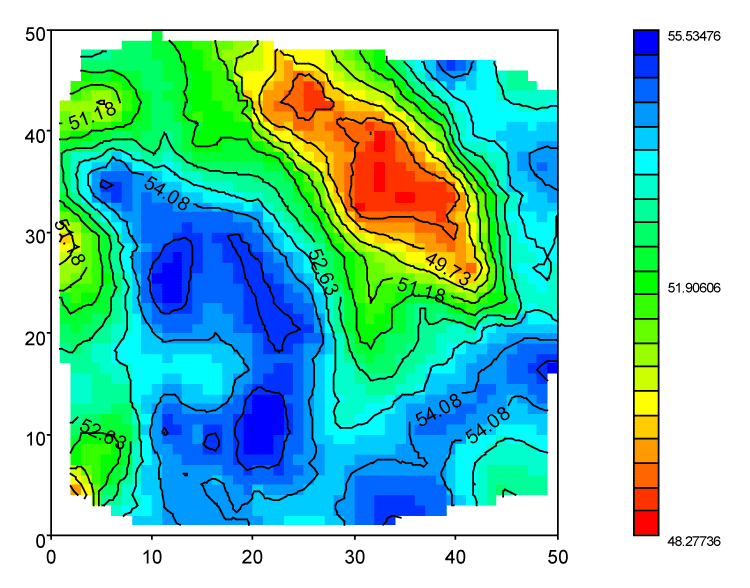
Nesta figura, pode-se verificar que a direção de maior continuidade do fenômeno espacial é N135, confirmando a informação fornecida pelo mapa variograma. Nesta direção, a variabilidade é menor que na direção ortogonal N45. Trata-se de um entendimento importante, pois trabalhos futuros poderão ser orientados conforme essas direções, por exemplo, menor densidade amostral na direção de maior continuidade.

A krigagem foi o primeiro método a proporcionar uma medida da incerteza, por meio da variância de krigagem, que pode ser calculada conforme (Yamamoto, 2020, p. 197):

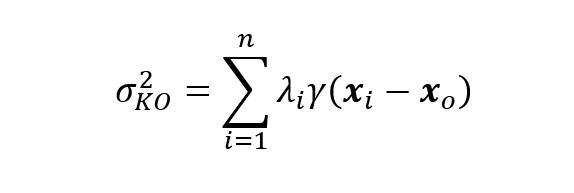
Onde γ(x_i–x_o) é o resultado da função variograma calculado entre o i-ésimo ponto e o centro da célula da malha regular.

Na Figura 6, ilustra-se o desvio padrão de krigagem que é a raiz quadrada da variância de krigagem.

Neste mapa, é possível verificar que nos pontos de dados, a incerteza é pequena e aumentando quando se distancia dos pontos de dados. Além disso, nesse caso específico, reflete também a orientação N135, que é a direção de maior continuidade do fenômeno espacial.

Considerações finais

Este artigo mostrou uma aplicação direta da geoestatística, conforme os dois objetivos principais definidos por Matheron (1971, p. 5): em base teórica, expressar as propriedades estruturais em uma forma adequada (variograma) e em termos práticos, resolver os problema de estimativa de uma variável regionalizada a partir dos dados amostrais (krigagem). O Leitor poderá adaptar o roteiro apresentado para os dados de sua área de conhecimento.

Referências bibliográficas

Caers, J. 2011. Modeling uncertainty in the Earth Sciences. Sussex, Wiley-Blackwell. 229p.

David, M. 1977. Geostatistical ore reserve estimation. Amsterdam, Elsevier. 363p.

Journel, A.G.; Huijbregts, C.J. 1978. Mining geostatistics. New York, Academic Press. 600p.

Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo. Gráfica Paulo’s. 308p.

Yamamoto, J.K.; Landim, P.M.B. 2013. Geoestatística: conceitos e aplicações. São Paulo, Oficina de Textos. 215p.