Como calcular variogramas experimentais para dados com distribuição irregular (Parte 2)

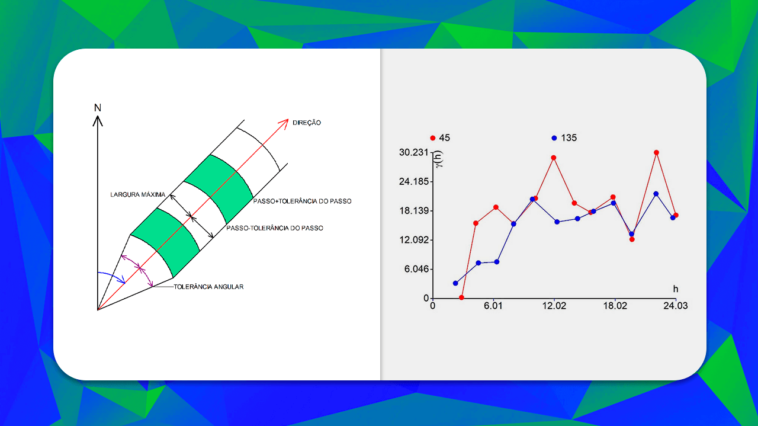
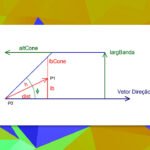
No artigo anterior, apresentamos a função varPares() que permite determinar os pares de pontos que satisfazem os critérios de direção ± tolerância angular e passo ± tolerância do passo (Figura 1). Em continuidade, este artigo irá apresentar a classificação dos pares de pontos para o cálculo de variogramas experimentais.

Neste artigo, iremos fazer a classificação dos pares de pontos para definição da função variograma e sua representação no dispositivo gráfico.

Scripts utilizados

O Script GKS10sim2.R incorpora o código apresentado anteriormente (Script GKS10sim1.R), mas iremos apresentar e comentar apenas a parte correspondente ao presente artigo, ou seja, a partir da linha 36.

Parte 3

A classificação dos pares de pontos para fins de cálculo da função variograma é uma etapa importante, pois a programação envolvida deve ser eficiente e sempre que possível evitando comandos condicionais. Observe-se que nesta função se usa apenas dois comandos condicionais.

Na linha 39, define-se a variável delta, que é a diferença entre pmax e pmin, multiplicada por 1,0000001. Este artifício garante que todos os valores calculados na linha 49 estarão entre 1 e npassos.

Isso significa que não há necessidade de se testar a cada valor calculado se é maior que 1 e menor ou igual a npassos. A classificação dos pares de pontos é feita entre as linhas 45-54.

Os objetos usados são: pairs, d e gama, que servem para armazenar cumulativamente os pares, as distâncias e diferenças ao quadrado, respectivamente. Em seguida, os valores médios de distância e função variograma são calculados nas linhas 55-61.

Parte 4

Agora, podemos aplicar a função varClasses(), conforme a parte 4 do Script GKS10sim1.R.

A função varClasses() é chamada nas linhas 78-79, onde os resultados são armazenados no objeto res. Os resultados são transferidos para um vetor chamado gamaDat que guarda os valores conforme a direção, passo e valores (distância, função variograma e número de pares).

Este Autor prefere usar vetores ao invés de matrizes para armazenamento de valores que dependem do número de variáveis (ndir – número de direções e npassos – número de passos), como se pode verificar na linha 73.

Além disso, a parte 4 contempla a função recKC(), que permite recuperar os valores individuais de distância, função variograma e número de pares a partir do vetor gamaDat.

Parte 5

Continuando, passaremos a descrever e comentar a parte 5 do Script GKS10sim2.R. Devido à extensão desta parte, faremos a descrição por trechos. O primeiro trecho (linhas 95-123) prepara a plotagem do variograma no dispositivo gráfico do seu computador. Se preferir que o desenho seja gravado em arquivo tipo Jpeg, basta tirar os comentários (#) das linhas 99-100 e 144). Entre as linhas 102-104, cria-se uma área de plotagem em branco, pois queremos o desenho da função variograma feito por programação, ao invés de se usar uma função de alto nível, que no caso seria a própria função plot(). Na verdade, ao optarmos pelo uso da função plot() como uma função de baixo nível, nos dá mais liberdade para personalizar as saídas gráficas.

Em seguida, desenha-se os eixos X e Y com as respectivas divisões e anotações, conforme as linhas 105-123.

O segundo trecho se refere à plotagem dos pontos do variograma experimental (linhas 124-131). Observe-se na linha 125 que se define o objeto cor com quatro cores. Caso o Leitor queira processar maior número de direções, deve-se adequar o vetor cor com mais cores (linha 125). Nas linhas 127-128, chama-se a função recKC() que permite recuperar os dados armazenados no vetor gamaDat.

No trecho seguinte, a legenda dos variogramas é desenhada nas linhas 132-138. Por fim, o último trecho (linhas 139-143) identifica os eixos do variograma.

Executando o script GKS10sim2.R, tem-se o resultado apresentado na Figura 2. Nesta figura, pode-se verificar que os variogramas configuram uma anisotropia mista, sendo que a direção 135º deve representar a direção de maior continuidade (menor patamar). A modelagem do variograma será tratado em artigos futuros.

Considerações finais

Este artigo completa a apresentação do script que permite calcular variogramas experimentais para uma dada direção, dados a tolerância angular, largura da banda, passo e tolerância do passo para um número de passos.

Como se descreve no primeiro artigo, trata-se de uma nova aproximação com base em recursos da álgebra linear. Este algoritmo foi extraído a partir do sistema SGeMS (Remy et al. 2009).

Destaca-se a possibilidade de se definir a largura da banda para limitar os pares dentro de uma área razoável. Sem isso, há o risco do variograma não refletir corretamente a função variograma para uma dada direção, devido à abertura do indefinida do cone de pesquisa (Figura 1).

Referências bibliográficas

Remy, N.; Boucher, A.; Wu, J. 2009. Applied geostatistics with SGeMS. New York, Cambridge University Press. 264p.

Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 344p.

Próximos artigos

Os próximos artigos irão tratar dos ângulos para correção da anisotropia.