Cálculo de variogramas experimentais para dados com distribuição irregular: parte 1

A aplicação da conhecida equação para o cálculo de variogramas experimentais requer pares de pontos separados por uma distância h, como se pode verificar:

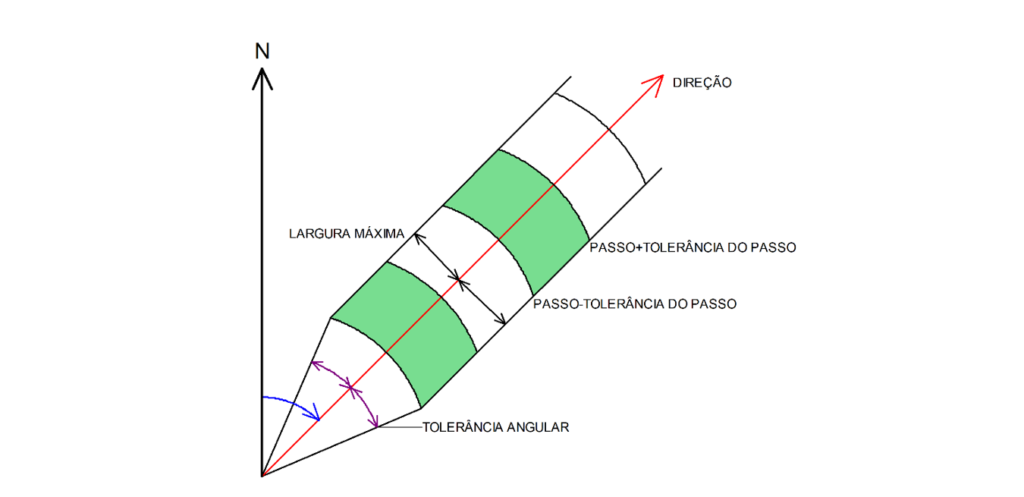
Para dados com distribuição irregular, em qualquer direção os pontos não estão separados exatamente por uma distância h. Assim, nesses casos se aplica um dispositivo geométrico que permite localizar pares de pontos situados dentro de uma área definida pela direção mais ou menos a tolerância angular e passo mais ou menos a tolerância do passo (Figura 1).

Cálculo de variogramas experimentais

O cálculo de variogramas experimentais é uma fase crítica na análise geoestatística, pois pode representar um tempo excessivamente longo de processamento, dependendo da quantidade e distribuição de pontos e, principalmente do algoritmo aplicado.

Neste artigo, vamos abordar o algoritmo para o cálculo de variogramas experimentais baseado no Sistema SGEmS (Remy et al. 2009). Trata-se de uma aproximação atualizada com aplicação dos conceitos de álgebra linear, como se poderá verificar na função varPares() em linguagem R.

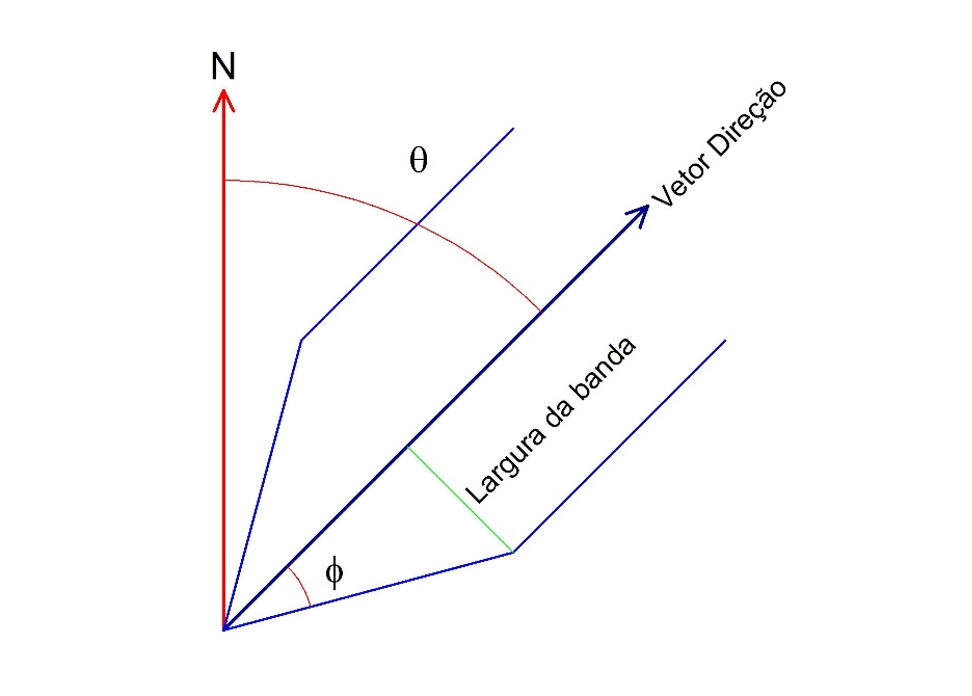
Para descrever o algoritmo de Remy et al. (2009), necessita-se definir os ângulos ϴ e Ф em graus, direção e tolerância angular, respectivamente e a largura da banda (Figura 2). A direção medida a partir do N no sentido horário (azimute) determina o vetor direção. A largura da banda é uma distância estabelecida para delimitar a pesquisa de pares de pontos e equivale ao raio da base do cone. O dispositivo geométrico é posicionado em um ponto de dado para localizar o outro ponto que forma o par de pontos que satisfaz os critérios estabelecidos em termos direção mais ou menos a tolerância angular e passo mais ou menos a tolerância do passo (Figura 2).

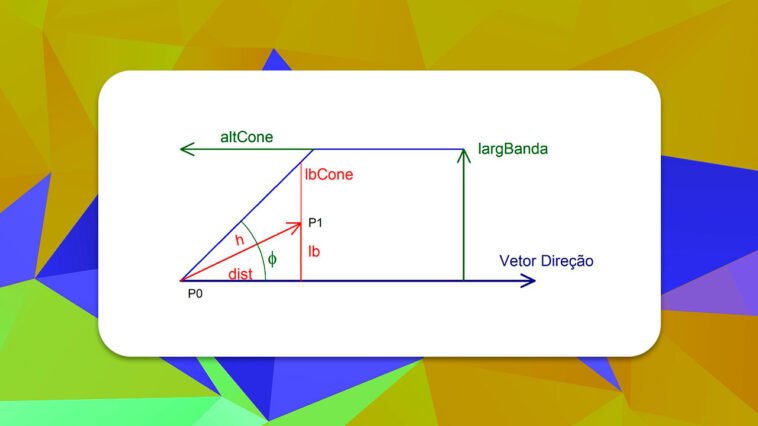
Continuando, faz-se a rotação do vetor direção (Figura 1) para o eixo X e se representa apenas a metade da banda (Figura 3).

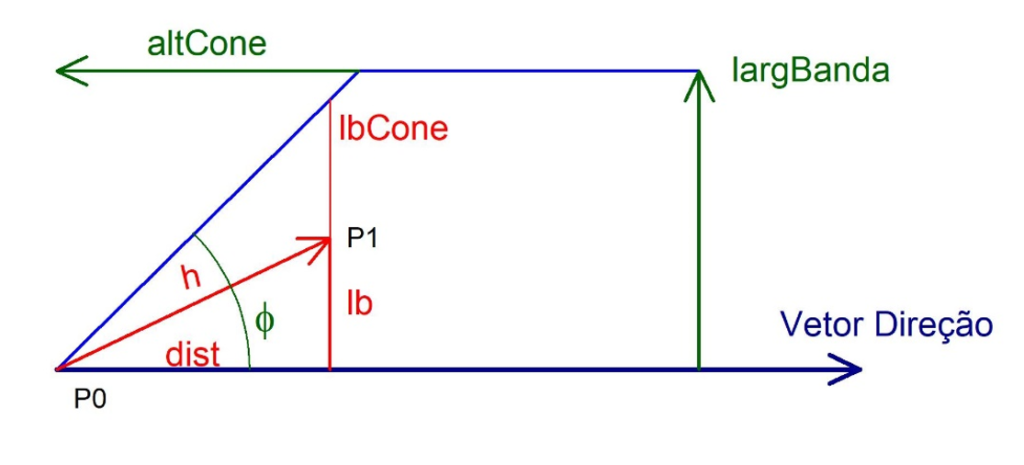
A partir da Figura 3, observa-se que:

Além do vetor direção (v_d), tem-se o vetor ponto (v_p) definido entre os pontos P0 e P1. A distância h é a hipotenusa do triângulo retângulo, que tem como catetos dist e lb (Figura 3). Assim, pelo Teorema de Pitágoras:

A tangente da tolerância angular pode ser calculada como:

Por conveniência, vamos usar o quadrado de lbCone:

Por outro lado, o cateto dist é o resultado do produto escalar do vetor direção (v_d) pelo vetor ponto (v_p):

Lembrando que o produto escalar:

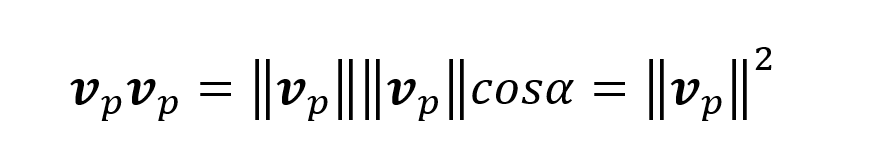
Desse modo, tem-se:

E, portanto:

Assim, na ilustração da Figura 3, pode-se verificar que o ponto P1 está dentro da tolerância angular, pois:

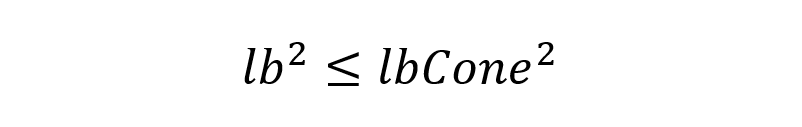
As condições para verificação se o ponto está dentro do dispositivo são:

• Se (dist > altCone) & (lb² < largBanda²) “ponto dentro”
• Se (dist ≤ altCone) & (lb² < lbCone²) “ponto dentro”
• Caso contrário “ponto fora”

A função varPares() gera uma lista de pares de pontos que satisfazem as condições de verificação. Como a função variograma é calculada sobre as distâncias h, deve-se fazer a classificação dos pares de pontos em termos do passo ± tolerância do passo, que é realizada pela função varClasses().

Script GKS10sim1.R

Neste artigo, oferecemos o Script GKS10sim1.R que permite calcular os pares de pontos de variogramas experimentais em duas direções (45 e 135º) para o conjunto de dados simetrica49.csv. Para executar o script, deve-se disponibilizar os arquivos de entrada: simetrica49.csv e simetrica49_varpar.csv (arquivo de parâmetros).

O arquivo de parâmetros é fornecido como um data frame (Figura 4), que deve conter seis colunas: direção, tolerância angular, largura da banda, passo, tolerância do passo e número de passos.

Ao executar o script, o Leitor irá verificar que os pares de pontos são listados no console. Esses pares estão sempre ordenados: (i, j), de tal forma que j > i. Isso ocorre porque o dispositivo geométrico (Figura 1) é centrado no ponto i, a partir do qual se pesquisa o ponto j (j > i) que satisfaz as condições de verificação (direção ± tolerância angular e passo ± tolerância do passo), vide Figura 5 que mostra os primeiros 20 pares.

Considerações finais

Este artigo apresentou o processo de determinação dos pares de pontos que satisfazem os critérios de localização: direção ± tolerância angular e passo ± tolerância do passo. O algoritmo implementado, com base em Remy et al. (2009), representa uma aproximação moderna baseada em conceitos de álgebra linear. Trata-se de uma evolução em relação aos algoritmos anteriormente publicados, por exemplo, Deutsch e Journel (1992).

Próximo artigo

No próximo artigo, vamos usar os pares determinados pela função varPares() para calcular a função variograma e fazer sua representação no dispositivo gráfico.

Referências bibliográficas

Deutsch, C.V.; Journel, A.G. 1992. GSLIB – Geostatistical software library and user’s guide. New York, Oxford University Press. 340p.

Remy, N.; Boucher, A.; Wu, J. 2009. Applied geostatistics with SGeMS. New York, Cambridge University Press. 264p. Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 344p.