Este artigo reproduz integralmente, com alguns ajustes, o conteúdo do item 2.7.5, do Capítulo 2: Conceitos de probabilidade e estatística do nosso livro: Estatística, Análise e Interpolação de dados geoespaciais (Yamamoto, 2020).
Além de disponibilizar o conteúdo em nosso blog, o artigo tem por objetivo mostrar como os assuntos são tratados no referido livro.
Neste artigo, vamos abordar a distribuição normal, que tem uma importância fundamental não apenas nas Ciências da Terra como também em outras áreas do conhecimento.
Distribuição normal
Resultados de muitos processos físicos e observações geológicas seguem uma distribuição normal (Borradaile, 2003, p. 70). A distribuição normal é a mais importante em todas as áreas de aplicação da estatística.
Na análise de dados geoespaciais, a distribuição normal também é muito usada não só porque a maioria das variáveis contínuas segue esse modelo teórico, mas também porque essa distribuição é muito conveniente por suas propriedades que são matematicamente conhecidas.
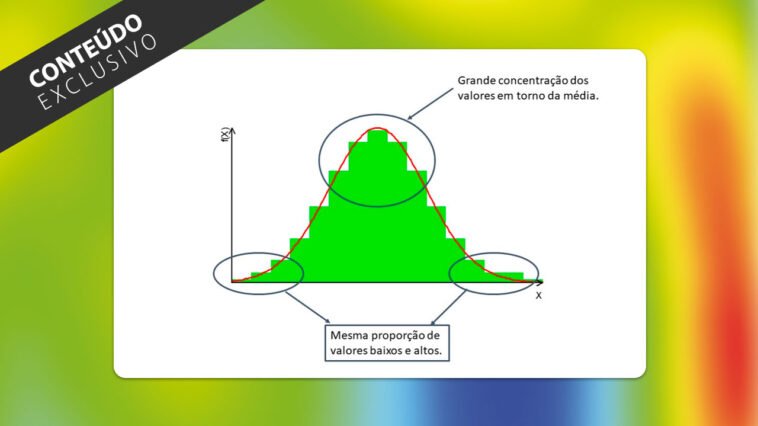
Além disso, a questão da simetria é uma propriedade importante para fins de interpolação de dados geológicos, pois há uma distribuição equitativa dos dados em torno da média (Figura 1).
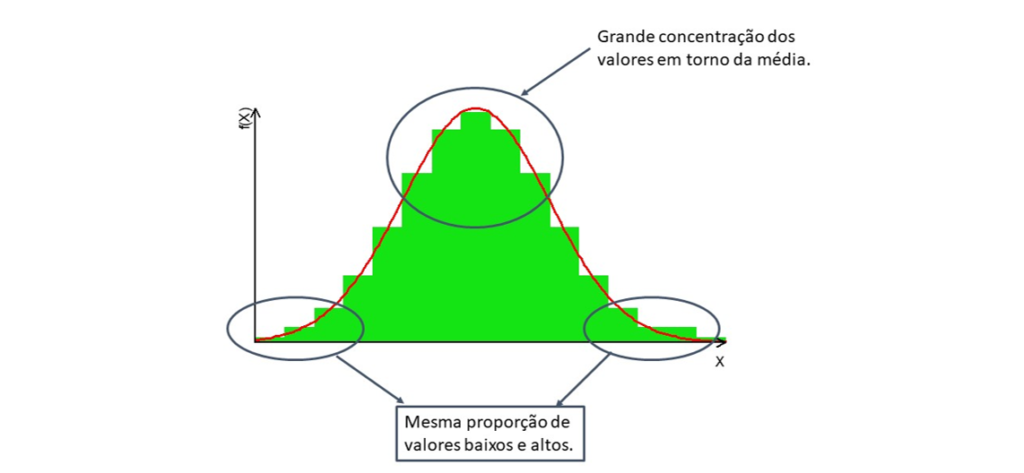
A distribuição normal combina tanto a variação natural do sistema como erros aleatórios da observação, ou seja, isso significa que a média e a variância fundem erros de medida com a variação inerente dos processos geológicos (Borradaile, 2003, p. 71). Segundo esse autor, as observações têm pequenos erros de medida quando comparados à variação natural do sistema.
Em estudos de inventários minerais, as distribuições normais são particularmente úteis para lidar com os vários tipos de erros, especialmente aqueles em análise e amostragem (Sinclair e Blackwell, 2002, p. 83).
Muitas vezes, os dados não seguem uma distribuição normal, mas após aplicação de uma transformação matemática, estes dados passam a apresentar as características desejáveis, tais como simetria na distribuição de frequências, com média igual a zero e variância unitária (e.g. Koch e Link, 1970, p. 36).
Um método extremamente simples para transformação de dados é denominado transformada escore normal (segundo Deutsch e Journel, 1992, p. 138), em que não importa a forma da distribuição inicial, pois a distribuição final será sempre normal com média zero e variância igual a um.
A distribuição normal tem um papel importante na inferência da média populacional a partir da média amostral (Lapin, 1998, p. 168).
Função densidade de probabilidade normal
A função densidade de probabilidade da distribuição normal é dada pela seguinte equação (Agterberg, 1974, p. 57):

Onde µ e σ são a média e o desvio padrão da distribuição normal, que especificam completamente a localização (média µ) e a escala da curva normal por meio do desvio padrão σ (Lapin, 1998, p. 169).
A distribuição normal é comumente utilizada para modelar dados de uma população ou de um experimento (Krishnamoorthy, 2016, p. 143).
Função de distribuição acumulada normal
A função de distribuição acumulada normal pode ser escrita como (Spiegel et al., 2013, p. 122; Hsu, 2014, p. 63):

Segundo Hsu (2014, p. 63), essa integral não pode ser avaliada analiticamente de forma fechada e deve ser computada numericamente por meio da função:

Segundo Krishnamoorthy (2016, p. 143), uma aproximação polinomial pode ser usada para calcular essa função:

Onde:
P0=913.167442114755700; P1=1024.60809538333800; P2=580.109897562908800;
P3=202.102090717023000; P4= 46.0649519338751400; P5=6.81311678753268400;
P6=6.047379926867041e-01; P7=2.493381293151434e-02;
Q0=1826.33488422951125; Q1=3506.420597749092; Q2=3044.771121163622200;
Q3=1566.104625828454; Q4=523.596091947383490; Q5=116.9795245776655;
Q6=17.1406995062577800; Q7=1.515843318555982; Q8=6.25e-02;
Essa equação pode ser usada para calcular as áreas sob a curva normal para os escores desejados. Por exemplo, a Figura 2 mostra as áreas calculadas para alguns escores normais, que significam as probabilidades de P(Z ≤ z). Esta expressão é usada para calcular as probabilidades acumuladas para a distribuição normal padrão.

A distribuição normal e o Teorema do Limite Central
A distribuição normal é um modelo matemático de dispersão comumente aplicado em geologia (Borradaile, 2003, p. 74). Além disso, ela tem uma importância extraordinária em estatística e geoestatística porque é a distribuição limite do teorema do limite central e é matematicamente tratável (Rossi e Deutsch, 2014, p. 25).
Os parâmetros µ e σ definem a forma da curva normal, como se ilustra na Figura 3.

As áreas sob as curvas normais fornecem probabilidades, que dependem apenas da distância entre a média µ e o ponto dado em unidades de desvio padrão σ (Lapin, 1998, p. 169). Por exemplo, a Figura 4 representa as áreas sob a curva normal para 1, 2 e 3 desvios padrão em torno da média.

As condições sob as quais uma variável aleatória segue uma distribuição normal são especificadas pelo Teorema do Limite Central (Haan, 1977, p. 89). Segundo esse autor, se Sn é a soma de n variáveis aleatórias idênticas e independentemente distribuídas Xi, cada uma com média µ e variância σ2, então no limite quando n tende ao infinito, a distribuição de Sn aproxima uma distribuição normal com média nµ e variância nσ2.
A variável aleatória Xn é a soma de n variáveis aleatórias:

Matematicamente, o Teorema do Limite Central pode ser descrito como (Spiegel et al. 2013, p. 112):

Onde

é a variável padronizada de Sn.
Considerações finais
Este artigo apresentou a distribuição normal, que é um modelo de distribuição de probabilidades da maior importância na análise de dados geoespaciais.
Lembrando que este artigo reproduz integralmente, com alguns ajustes, o conteúdo do item 2.7.5, do Capítulo 2: Conceitos de probabilidade e estatística do nosso livro: Estatística, Análise e Interpolação de dados geoespaciais (Yamamoto, 2020).
Adquira o livro e tenha acesso a todo esse conteúdo exclusivo!
Referências bibliográficas
Abramowitz, M.; Stegun, I.A. 1972. Handbook of mathematical function with formulas, graphs, and mathematical tables. New York, Dover Publications Inc. 1046p.
Agterberg, F.P. 1974. Geomathematics: Mathematical background and Geo-Science Applications. Amsterdam, Elsevier. 596p.
Borradaile, G. 2003. Statistics of earth science data. Heidelberg, Springer. 351p.
Deutsch, C.V.; Journel, A.G. 1992. GSLIB – Geostatistical software library and user’s guide. New York, Oxford University Press. 340p.
Haan, C.T. 1977. Statistical methods in hydrology. Ames, The Iowa State University Press. 378p.
Hsu, P.H. 2014. Probability, random variables, and random processes. New York, McGraw Hill. 422p.
Koch, G.S.; Link, R.F. 1970. Statistical analysis of geological data. New York, Dover Publications Inc. Vol. I. 375 p.; Vol. II. 438p.
Krishnamoorthy, K. 2016. Handbook of statistical distributions with applications. Boca Raton, CRC Press. 398p.
Lapin, L.L. 1998. Probability and statistics for modern engineering. Prospect Heights, Waveland Press. Inc. 810p.
Rossi, M.; Deutsch, C.V. 2014. Mineral resource estimation. Dordrecht, Springer. 332p.
Sinclair, A.J.; Blackwell, G.H. 2002. Applied mineral inventory. Cambridge, Cambridge University Press. 381p.
Spiegel, M.T.; Schiller, J.J.; Srinivasan, R.A. 2013. Probability and Statistics. New York, Mc Graw Hill. 424p.
Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 308p.
Próximo artigo
O próximo artigo, em continuidade a este, irá tratar da distribuição lognormal, que tem significado especial nas geociências, haja vista ser o modelo de distribuição de probabilidades de muitas variáveis, tais como: distribuição de frequências de fenômenos raros e metais nobres.