Distribuição lognormal

O que é a distribuição lognormal?

A distribuição lognormal representa um dos modelos teóricos de maior importância no estudo de depósitos minerais, pois ela explica a ocorrência de metais raros (Cu, W, Sn, Au, Ag etc.), diamante e urânio.

Na natureza, alguns fenômenos são tipicamente lognormais, como, por exemplo, a distribuição de terremotos em zonas tectonicamente ativas, onde há um grande número de terremotos de pequena magnitude, mas alguns altamente destrutivos.

Por definição, a distribuição lognormal é caracterizada pela propriedade que os logaritmos dos valores seguem uma distribuição normal (Koch e Link, 1970, p. 213).

Esta distribuição de frequências se caracteriza pela forte assimetria positiva, dada pela ocorrência de uma grande quantidade de valores baixos e uma pequena quantidade de valores altos a muito altos.

Em depósitos minerais, muitas vezes os valores altos ou muito altos não são completamente amostrados na pesquisa mineral e passam a ser conhecidos na fase da mineração.

Muitas vezes, esses valores altos são interpretados como valores anômalos e excluídos do conjunto de dados. Esse procedimento deve ser evitado na avaliação de recursos minerais, pois pode levar à subestimativa de parte do depósito mineral com teores significativos.

A distribuição lognormal é usada para modelar variáveis não negativas com assimetria positiva (Rossi e Deutsch, 2014, p. 14).

Função densidade de probabilidade lognormal

Levando em consideração a mudança de variável, a função densidade de probabilidade da distribuição lognormal pode ser desenvolvida a partir da seguinte relação (Agterberg, 1974, p. 194):

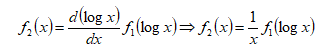
Onde    é a função densidade de probabilidade normal descrita pela equação:

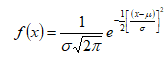
Substituindo esta equação em (1), tem-se (Agterberg, 1974, p. 195):

Na equação (2), 

são respectivamente a média e o desvio padrão dos logaritmos de X. Novamente, µ e σ são os parâmetros da função densidade de probabilidade lognormal. Esses parâmetros controlam a forma da distribuição, ou seja, a localização e a assimetria da distribuição conforme o valor de σ. A Figura 5 mostra como o desvio padrão dos logaritmos afeta a assimetria.

Deve-se notar que nem todo o intervalo de variação foi representado na Figura 5B. A precisão das funções de densidade acumulada lognormal desenhadas pode ser conferida pela mediana igual a 1,649 para todas as distribuições (Figura 5B).

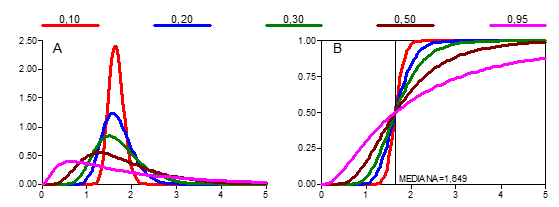
Figura 5: Distribuições lognormais para média dos logaritmos µ igual a 0,50 e
desvio padrão dos logaritmos s variável conforme legenda. Funções densidade de probabilidade (A)
e funções de densidade acumulada (B).

As médias, modas e variâncias correspondentes à variável aleatória X foram calculados com base nas seguintes equações (Yang, 2008, p. 124):

Esperança matemática:

Moda:

Mediana:

Variância:

Os resultados apresentados na Tabela 2 mostram claramente que a média se desloca à direita da moda, tanto quanto aumenta o CV ou o desvio padrão dos logaritmos de X.

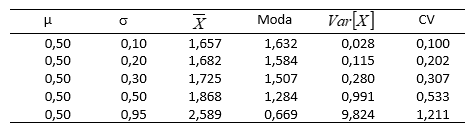
Tabela 2: Parâmetros da distribuição lognormal (µ e σ) e
estatísticas correspondentes à variável aleatória X.

Retomando os dados da distribuição com assimetria positiva abordada no item anterior, a Figura 6 apresenta os ajustes feitos com o modelo lognormal.

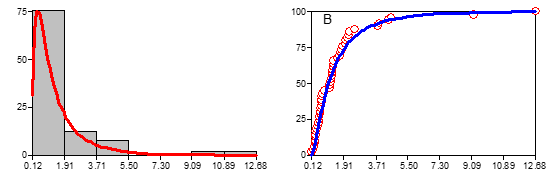
Figura 6: Ajustes da função densidade de probabilidade lognormal (A) e
função de densidade acumulada aos dados da distribuição com assimetria positiva.

Essa figura mostra que o modelo lognormal se ajusta perfeitamente aos dados com assimetria positiva, confirmando tratar-se de uma distribuição lognormal.

No próximo artigo falaremos a respeito da distribuição uniforme, cujo modelo é importante para entender o processo de Monte Carlo utilizado nas simulações geoestatísticas.

Quer aprender mais sobre as distribuições de frequências mais usadas em geologia e mineração?

Confira aqui nosso curso de Geoestatística: Fundamentos e Aplicações e aprenda muito mais desse universo.

Referências:

Agterberg, F.P. 1974. Geomathematics: mathematical background and geo-science applications. Amsterdam, Elsevier Scientific Publishing Company. 596p.

Koch, G.S.; Link, R.F. 1970. Statistical analysis of geological data. New York, Dover Publications Inc. Vol. I. 375 p.; Vol. II. 438p.

Rossi, M.; Deutsch, C.V. 2014. Mineral resource estimation. Dordrecht, Springer. 332p.

Yang, X. 2008. Mathematical modelling for Earth Sciencesd. Edinburgh, Dunedin Academic Press. 310p.