Distribuição normal

O que é a distribuição normal?

A distribuição normal é a mais importante dentre os modelos teóricos, pois explica a ocorrência de um grande número de variáveis aleatórias na natureza. Em geologia, teores de elementos maiores em rochas seguem a distribuição normal.

De acordo com o teorema do limite central, a distribuição das médias de amostras aleatórias retiradas de qualquer população segue uma distribuição normal, cuja tendência à normalidade torna-se mais pronunciada com o aumento do tamanho da amostra (Davis, 1986).

Além disso, devido à conveniência de se trabalhar matematicamente, a distribuição normal é a distribuição teórica mais usada na prática (Koch e Link, 1970). A função densidade de probabilidade da distribuição normal, para uma variável aleatória X com média µ e desvio padrão σ, é descrita pela seguinte equação (e.g. Agterberg, 1974):

As estatísticas µ e σ definem a forma da distribuição normal ou de Gauss. Na realidade, µ e σ são os parâmetros da função densidade de probabilidade normal. Por definição, uma distribuição normal tem média igual a zero e desvio padrão igual a um. Quanto maior o desvio padrão σ, maior o grau de achatamento da curva. A Figura 2 ilustra algumas distribuições com desvios padrão iguais a 1,0, 1,5 e 2,0 e média constante igual a zero.

Figura 2: Distribuições normais com médias iguais a zero e
desvios padrão iguais a 1,0 (vermelho); a 1,5 (azul) e 2,0 (verde).

Para as distribuições representadas na Figura 2 foram calculadas as amplitudes interquartis, conforme a Tabela 1.

Tabela 1: Amplitudes interquartis para as distribuições ilustradas na Figura 2.

Conforme se observa na Tabela 1, a amplitude interquartil aumenta com o desvio padrão, ou seja, com o espalhamento da distribuição em torno da média.

Usando os dados da Tabela 1, bem como a sua distribuição de frequências, foram feitas as representações do histograma e da curva acumulativa (Figura 3), nos quais foram ajustadas as funções densidade de probabilidade simples e acumulada.

Figura 3: Distribuição de frequências e ajuste da função densidade de probabilidade normal (A)
e curva acumulativa com ajuste da função de distribuição acumulada normal (B).

A função de distribuição acumulada normal (Figura 4B) é a integral da função densidade de probabilidade: 

onde  . O fator é usado para normalização das densidades de probabilidade (Yang, 2008).

Essa equação foi aproximada como (Abramowitz e Stegun, 1965):

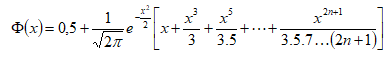
onde n é o número de termos considerado para fazer a aproximação. Nesse trabalho, o número de termos será igual a 100.

Como se pode observar na Figura 3, o modelo normal se ajusta perfeitamente aos pontos de dados, concluindo-se, portanto, que os dados seguem uma distribuição bem próxima da normal. Apenas para fins comparativos, os dados com assimetria positiva e assimetria negativa foram representados juntamente com os respectivos modelos teóricos normais (Figura 4).

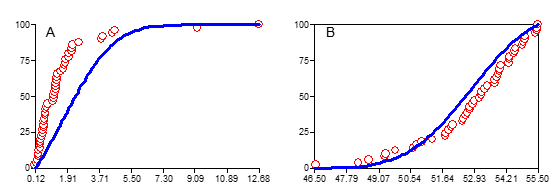
Figura 4: Curvas acumulativas e modelos normais ajustados para dados
com assimetria positiva (A) e para dados com assimetria negativa (B).

Verifica-se que os modelos normais não são adequados, notadamente para a distribuição de frequências com assimetria positiva.

Referências:

Abramowitz, M.; Stegun, I.A. 1965. Handbook of mathematical functions. New York, Dover Publications. 1046p.

Agterberg, F.P. 1974. Geomathematics: mathematical background and geo-science applications. Amsterdam, Elsevier Scientific Publishing Company. 596p.

Davis, J.C. 1986. Statistics and data analysis in geology. New York, John wiley & Sons. 646p.

Yang, X. 2008. Mathematical modelling for Earth Sciencesd. Edinburgh, Dunedin Academic Press. 310p.

Koch, G.S.; Link, R.F. 1970. Statistical analysis of geological data. New York, Dover Publications Inc. Vol. I. 375 p.; Vol. II. 438p.