Geoestatística para Engenheiros e Geocientistas (Olea, 1999)
Geoestatística para Engenheiros e Geocientistas (Olea, 1999)
Em 1999, Ricardo A. Olea publica seu livro intitulado “Geoestatística para Engenheiros e Geocientistas”.

Este livro é composto por 14 capítulos:
- Introdução;
- Krigagem simples;
- Normalização;
- Krigagem ordinária;
- O semivariograma;
- Krigagem universal;
- Validação cruzada;
- Deriva e resíduos;
- Simulação estocástica;
- Confiabilidade;
- Estimadores da distribuição acumulativa;
- Krigagem de bloco;
- Cokrigagem ordinária
- Classificação regionalizada.
Trata-se de uma obra apresentada com todo o rigor matemático, por meio de definições, lemas, teoremas e corolários.
Veja também: Retrospectiva da Geoestatística XI: Glossário da Geoestatística e Dicionário Multi-idiomas (Olea, 1991)
Krigagem simples (“Simple Kriging“)
O Capítulo 2, intitulado “Krigagem simples”, começa apresentando a fronteira convexa (Figura 1) que, segundo Olea (1999, p. 7), deve limitar a região de interesse para fins de estimativa geoestatística.
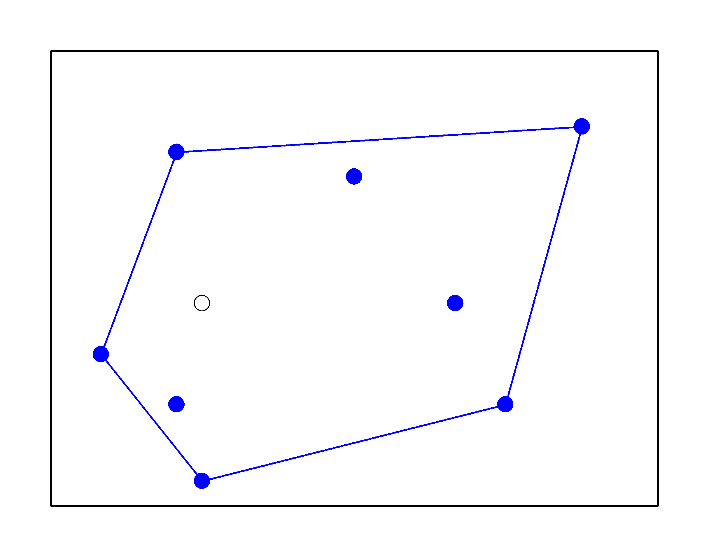
Olea (1999, p. 8-10) desenvolve as propriedades da combinação linear de variáveis para chegar à sua variância, que é utilizada para o cálculo da variância de estimativa dando origem ao sistema de equações de krigagem simples.
O Capítulo 3 descreve o processo de transformação Gaussiana por meio da técnica dos escores normais (Olea, 1999, p. 33-35).
Krigagem ordinária (“Ordinary Kriging“)
No Capítulo 4, Olea (1999, p. 39) começa o desenvolvimento da krigagem ordinária com a suposição que a amostragem é uma realização parcial da função aleatória Z(x). Assim, este autor determina a esperança da função aleatória que é suposta constante, que permite chegar à expressão da covariância para pontos separados por uma distância h.
Continuando o desenvolvimento, Olea (1999, p. 41) demonstra como se chega à fórmula da função variograma 2ϒ(h). Em seguida, desenvolve a expressão da variância de estimativa, que é a função objetivo que deve ser minimizada para se encontrar os pesos da krigagem ordinária (Olea, 1999, p. 45-51).
Semivariograma
No capítulo 5, o autor trata do semivariograma, pois conforme demonstrado nos algoritmos anteriores, a krigagem não é possível sem o conhecimento do semivariograma ou da covariância (Olea, 1999, 67). Tanto o semivariograma como a covariância se referem à taxa de variação espacial da função aleatória, enquanto o primeiro é uma função crescente a última é decrescente (Olea, 1999, p. 69).
A krigagem universal (“Universal Kriging“)
O Capítulo 6 é dedicado à krigagem universal, que permite fazer a estimativa na presença de uma tendência. Na realidade, a variável aleatória pode ser decomposta em termos da sua tendência e a variação local do atributo, como ilustra a Figura 2 (Olea, 1999, p. 92-93).

Com relação à krigagem universal, Olea (1999, p. 107) afirma que o principal problema desta técnica é a especificação do variograma, que deve ser o variograma residual. Segundo esse autor, a maneira mais fácil para estimar o variograma residual é fazer a modelagem de variogramas em direções livres da tendência.
Validação cruzada (“Crossvalidation“)
A validação cruzada é apresentada no Capítulo 7, onde o autor, ao analisar os resíduos ou os erros de estimativa, propõe o coeficiente de simetria (Olea, 1999, p. 120):
![]()
Onde é a moda amostral e a média amostral, p5 e o p95 são os percentis a 5 e 95% da distribuição. Segundo Olea (1999, p. 120), o coeficiente de simetria é menos sensível que o coeficiente de assimetria.
No Capítulo 8, o autor desenvolve o estimador da tendência, como uma componente de baixa frequência da variável regionalizada.
O Capítulo 9 aborda a simulação estocástica que, segundo Olea (1999, p. 141), não é a solução perfeita para o problema da suavização das estimativas de krigagem ordinária.
Confiabilidade (“Reliability“)
A questão da confiabilidade é tratada no Capítulo 10. Segundo Olea (1999, p. 163), uma vez conhecida a função de distribuição acumulada, pode-se definir limites de confiança da estimativa. Nesse capítulo, o autor analisa as aproximações para determinação das funções de distribuição acumulada com base tanto na krigagem indicadora como também nas realizações da simulação estocástica.
No capítulo seguinte, Olea (1999, p. 179) trata da questão de determinação da esperança condicional, ou seja, o estimador do tipo-E.
Em seguida, nos Capítulos 12 e 13, o autor desenvolve a krigagem de bloco e a cokrigagem ordinária, respectivamente.
Classificação Regionalizada (“Regionalized Classification“)
No capítulo 14, o tema da classificação regionalizada é introduzido. Segundo Olea (1999, p. 237), o objetivo da classificação regionalizada é explorar a suposição que as observações formam agrupamentos distintos no espaço, procurando os grupos que são homogêneos internamente e tanto quanto diferentes um do outro.
A exemplo dos livros textos anteriores, Olea (1999, p. 267-287) apresenta quatro conjuntos de dados denominados: aquífero Dakota (Figura 3A), aquífero de High Plains (Figura 3B), UNFC (Figura 3C) e campo de West Lyons (Figura 3D).
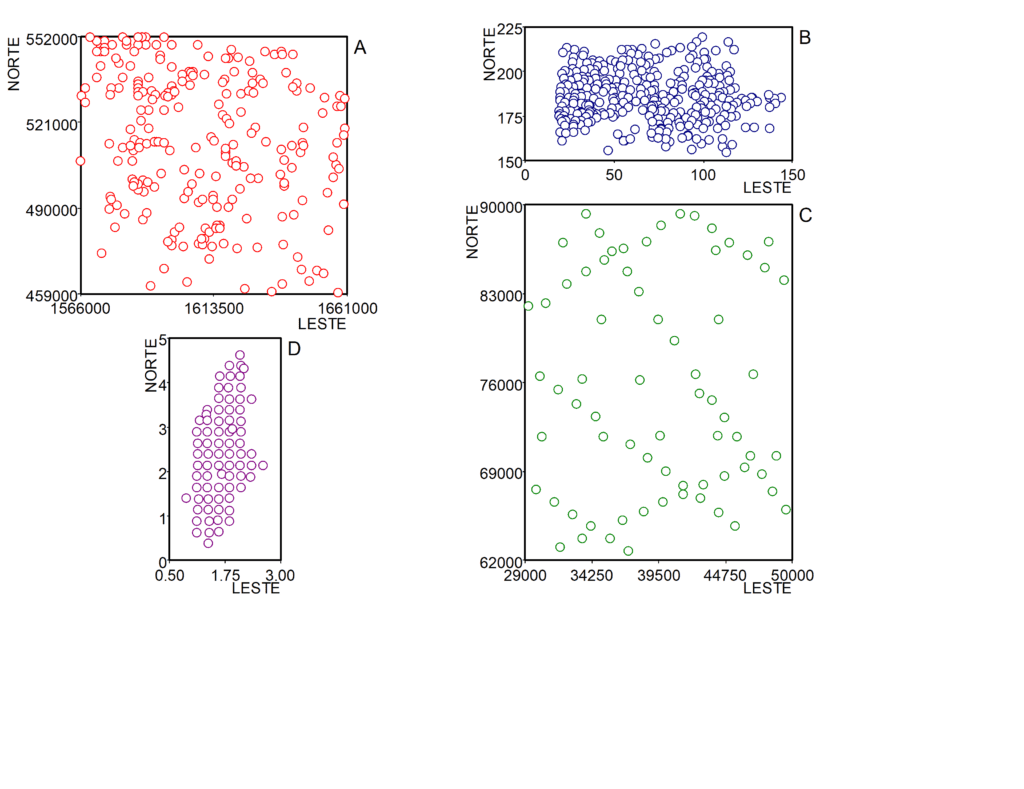
Referência
OLEA, Ricardo A. Geostatistics for Engineers and Earth Scientists. Norwell, Kluwer Academic Publishers, 1999. 303p.
Leia a primeira resenha da série:
Retrospectiva da Geoestatística I: Tratado de Geoestatística Aplicada (Matheron)


Deixe um comentário
Você precisa fazer o login para publicar um comentário.