Classificação de Recursos e Reservas Minerais – Parte 4: Avaliação Semiquantitativa da Confiabilidade Geológica

Como avaliar o que é conhecimento geológico na classificação de recursos minerais.

Série de artigos: Classificação de Recursos Minerais

Classificação de Recursos e Reservas Minerais Parte 1: Parâmetros de Classificação (CBRR)

Classificação de Recursos e Reservas Minerais Parte 2: Continuidade Geológica e de Teores

Classificação de Recursos e Reservas Minerais – Parte 3: Incertezas da Krigagem Ordinária

Classificação de Recursos e Reservas Minerais – Parte 4: Avaliação Semiquantitativa da Confiabilidade Geológica

No artigo anterior, foi apresentada a questão da incerteza associada à estimativa por krigagem ordinária. Foram introduzidas as aproximações existentes para quantificação da incerteza: variância de krigagem e variância de interpolação.

Neste artigo, vamos apresentar uma aproximação para avaliação semiquantitativa da continuidade geológica. Cabe ressaltar que o ideal seria uma medida de incerteza combinada derivada da geologia e de teores, mas isso ainda permanece como assunto para pesquisa futura.

O que é confiabilidade geológica

O fator chave na classificação de recursos e reservas minerais está associado ao conhecimento crescente da geologia, ou seja, a confiabilidade geológica. A confiabilidade geológica aumenta com o desenvolvimento da exploração mineral, cujos resultados permitem estabelecer a continuidade da mineralização e, consequentemente, a classificação dos recursos minerais em níveis crescentes de confiança. Os dados das sondagens são interpretados e integrados para a geração de um modelo geológico consistente da mineralização.

O modelo geológico deve ser a base para avaliação da continuidade geológica. Nesse sentido, a importância da modelagem geológica pode ser revisada, conforme a literatura internacional.

A importância da modelagem geológica

A modelagem de recursos e reservas minerais é geralmente concentrada no estabelecimento de domínios que englobam zonas mineralizadas geologicamente coerentes e estatisticamente homogêneas, as quais são baseadas na interpretação geológica tridimensional de um depósito (Duke e Hanna, 2001, p. 148 e Mackenzie e Wilson, 2001, p. 115). A geologia é uma área onde os princípios da boa prática recaem diretamente ao geólogo, cujo conhecimento, interpretação e entendimento das características da geologia e mineralização irão determinar o modelo geológico (Neuss, 2001, p. 54-55).

A importância do conhecimento geológico

Segundo Stephenson e Vann (2001, p. 13-14), qualquer resultado que não leve em conta a geologia pode resultar em uma avaliação errônea do valor do depósito mineral. A geologia aplicada ao desenvolvimento e lavra bem-sucedidos de um depósito mineral deve proporcionar simples respostas quantificáveis de combinações geológicas complexas de tonelagens, teores, qualidade da rocha e características de tratamento que são únicos em cada depósito (Mackenzie, 2001, p. 119).

Um fator chave na estimativa de um recurso mineral é a síntese de toda a informação geológica em um modelo geológico coerente, que deve considerar todos os elementos que podem influenciar a localização da mineralização (Stoker e Gilfillan, 2001, p. 32).

Determinação semiquantitativa da continuidade geológica

Como visto nos artigos anteriores, os fatores chaves para a classificação de recursos e reservas minerais são as continuidades: geológica, de teores e espacial. A continuidade geológica pode ser verificada diretamente no modelo geológico, que fornece a característica geológica para os blocos de estimativa. Assim, se o bloco estiver dentro da zona mineralizada, pode-se dizer que há continuidade geológica, caso contrário não. Por esse motivo, denomina-se avaliação semiquantitativa da continuidade geológica.

Para ilustrar esse conceito, a Figura 1 apresenta uma seção geológica, obtida de um modelo implícito. Nesta figura, os blocos em verde apresentam continuidade geológica (pertencem ao corpo mineralizado), enquanto os blocos em vermelho não apresentam.

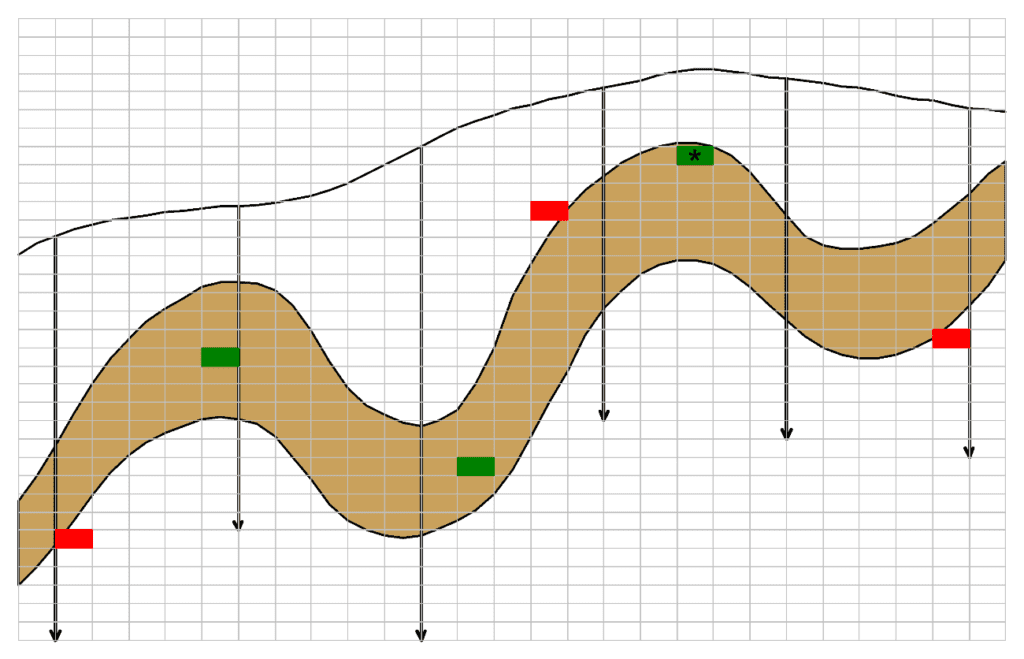
Como se pode verificar, os blocos pertencentes à camada mineralizada supostamente apresentam continuidade geológica. Como o modelo geológico é resultado da interpretação ou interpolação de dados geológicos, deve-se considerar também uma incerteza nos contatos geológicos, pois a forma interpretada pode não corresponder à realidade. Por exemplo, o bloco verde destacado com um asterisco, está situado em uma região que resulta de uma interpretação geológica e, consequentemente, está sujeita a incerteza. Assim, nesse caso, não é possível garantir a continuidade geológica.

Como mencionado anteriormente, o conhecimento geológico que é o fator chave na classificação de recursos minerais se adquire com a quantidade e qualidade da informação. Isso significa que há necessidade de se avaliar a quantidade de dados disponíveis na localização estimada. Esse parâmetro quantitativo só é possível pela aplicação do critério geométrico (espaçamento médio entre amostras ou sondagens e densidade amostral) que será visto nos artigos seguintes.

Como obter a continuidade geológica

A continuidade geológica pode ser extraída simplesmente do modelo geológico implícito ou explícito. Trata-se em fazer uso da informação geológica na classificação de recursos minerais. Evidentemente, o cálculo dos teores nos blocos do modelo tridimensional de blocos deve levar em consideração a litologia, fornecida pelo modelo geológico. Isso significa que a localização dos vizinhos próximos deve ser feita com restrição geológica, ou seja, apenas os vizinhos próximos que possuírem a mesma característica geológica do bloco para estimativa serão considerados. Esta modelagem integrada garante a maior confiabilidade nos teores estimados, resultando em um modelo de teores mais próximo da realidade amostral.

Avaliação do bloco com restrição da geologia

Os blocos de estimativa, que apresentam continuidade geológica, são avaliados restringindo a busca dos vizinhos próximos para as sondagens contidas no corpo mineralizado. Isso garante uma estimativa integrada com a geologia. No caso do exemplo apresentado na Figura 4.1, a pesquisa dos vizinhos próximos deve ser feita levando em conta a anisotropia variando localmente. A Figura 4.2 representa três blocos (vermelho, azul e verde) que precisam ser estimados usando a informação dos vizinhos próximos. Para os blocos vermelho e azul, os vizinhos próximos estão contidos na própria litologia de interesse, mas para o bloco verde, o procedimento localiza amostras da sondagem DH#4 pertencentes à outra litologia. Assim, além da anisotropia local, há necessidade de se restringir a pesquisa somente às amostras que sejam da mesma litologia do bloco sob estimativa. Portanto, trata-se de fazer uma pesquisa com restrição estrutural (anisotropia local) e geológica (litologia).

Esse exemplo mostra claramente que a anisotropia local ou dinâmica ainda não é a solução perfeita para modelagem de camadas dobradas. O desdobramento (unfold) poderia ser uma opção para esta situação. Porém, esse processo deve ser avaliado em situações críticas.

 

Próximo artigo

No próximo artigo serão revistos os esquemas de classificação de recursos minerais, notadamente aqueles usados na indústria da mineração. Serão apresentados os critérios geométricos para classificação de recursos minerais: distância da amostra mais próxima ao bloco; distribuição dos pontos em torno do bloco; variância de krigagem; espaçamento médio e densidade amostral. A variância de krigagem será apresentada como um índice de configuração espacial, ou seja, como um critério geométrico e não como uma medida de incerteza associada à estimativa.

Referências bibliográficas

Duke, J.H.; Hanna, P.J. 2001. Geological interpretation for resource modelling and estimation. In: Mineral Resources and Ore reserve Estimation – The AusIMM Guide to a Good Practice (Ed. A.C. Edwards) p. 147-156. Melbourne, The Australasian Institute of Mining and Metallurgy.

Mackenzie, D.H. 2001. Tonnes, grades and economics – The ZC experience 1985-1988. In: Mineral Resources and Ore reserve Estimation – The AusIMM Guide to a Good Practice (Ed. A.C. Edwards) p. 119-124. Melbourne, The Australasian Institute of Mining and Metallurgy.

Mackenzie, D.H.; Wilson, G.I. 2001. Geological interpretation and geological modelling. In: Mineral Resources and Ore reserve Estimation – The AusIMM Guide to a Good Practice (Ed. A.C. Edwards) p. 111-118. Melbourne, The Australasian Institute of Mining and Metallurgy.

Neuss, I. 2001. Oktokumpu – base metals best practice. In: Mineral Resources and Ore reserve Estimation – The AusIMM Guide to a Good Practice (Ed. A.C. Edwards) p. 49-56. Melbourne, The Australasian Institute of Mining and Metallurgy.

Stephenson, P.R.; Vann, J. 2001. Common sense and good communication in mineral resource and ore reserve estimation. In: Mineral Resources and Ore reserve Estimation – The AusIMM Guide to a Good Practice (Ed. A.C. Edwards) p. 13-20. Melbourne, The Australasian Institute of Mining and Metallurgy.

Stoker, P.T.; Gilfillan, J.F. 2001. The resource database. In: Mineral Resources and Ore reserve Estimation – The AusIMM Guide to a Good Practice (Ed. A.C. Edwards) p. 31-36. Melbourne, The Australasian Institute of Mining and Metallurgy.