Como classificar recursos e reservas minerais
Série de artigos: Classificação de Recursos e Reservas Minerais
Classificação de Recursos e Reservas Minerais Parte 1: Parâmetros de Classificação (CBRR)
Classificação de Recursos e Reservas Minerais Parte 2: Continuidade Geológica e de Teores
Classificação de Recursos e Reservas Minerais – Parte 3: Incertezas da Krigagem Ordinária
Critérios para classificar recursos e reservas minerais
Uma vez calculado o modelo de blocos com os teores da variável de interesse, o próximo passo é a classificação dos recursos e reservas minerais. Cada bloco desse modelo contém a informação básica do teor, bem como da incerteza associada (variância de krigagem ou de interpolação).
Porém, essas informações não são suficientes para fins de classificação, pois outras variáveis devem ser consideradas:
- distância da amostra mais próxima ao bloco;
- distribuição dos pontos em torno do bloco;
- variância de krigagem;
- espaçamento médio e
- densidade amostral.
Geralmente, a classificação dos blocos é feita por pós-processamento, segundo um critério escolhido pela Pessoa Competente.
Distância da amostra mais próxima em relação ao bloco
Segundo Rossi e Deutsch (2014, p. 217), muitas variações desse conceito foram usadas, mas a forma mais simples consiste em calcular a distância do centro do bloco para a amostra mais próxima usada na interpolação. Geralmente, conforme Sinclair e Blackwell (2002, p. 329), um raio pequeno é aplicado para definir um cilindro de material que é colocado na categoria de alta qualidade (Figura 1).
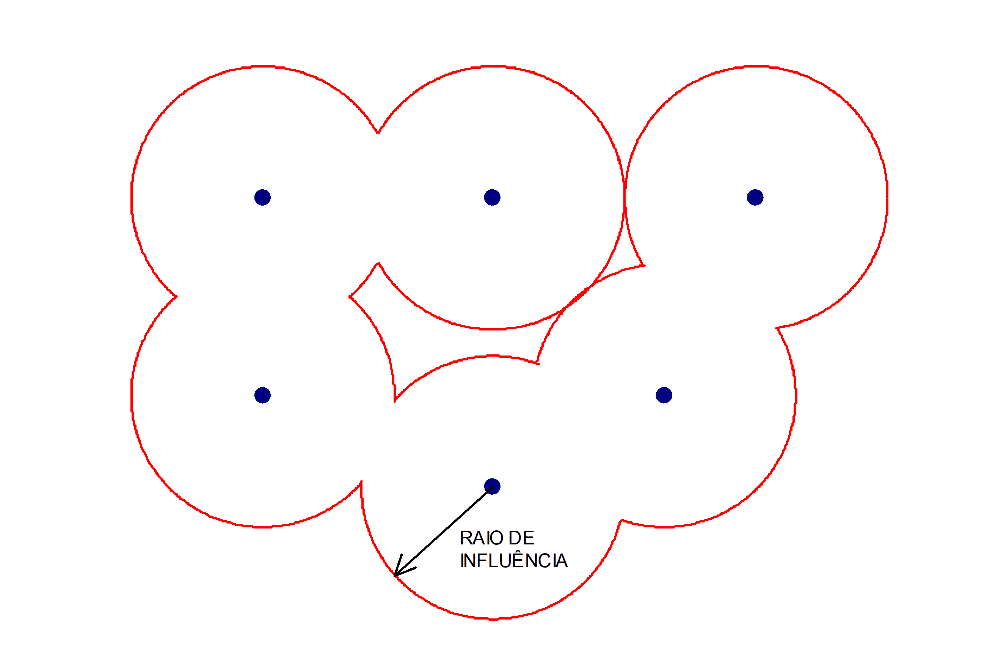
Distribuição de pontos em torno do bloco
A quantidade de pontos para estimativa de um bloco deve ser definida (por exemplo, um ponto por octante), bem como o número mínimo de pontos (por exemplo, no mínimo três octantes com pontos) são as condições para estimativa de um bloco.
Entretanto, elas não são suficientes para classificação, pois todos os blocos do modelo tridimensional serão calculados usando uma vizinhança entre o mínimo e o máximo. Mas, deve-se diferenciar blocos conforme a distribuição dos pontos amostrais em relação ao bloco estimado (Figura 2).

Interpolação x Extrapolação
Segundo Sinclair e Blackwell (2002, p. 329), existe uma diferença significativa entre n amostras de um lado do bloco a ser estimado (extrapolação) e n amostras distribuídas em torno do bloco a ser estimado (interpolação).
Assim, as classes de maior confiança deveriam ser atribuídas a blocos interpolados, enquanto aqueles extrapolados deveriam receber classes de menor confiança (Sinclair e Blackwell, p. 329-330).
Variância de krigagem
A variância de krigagem foi muito usada no passado para fins de classificação de recursos minerais (Rossi e Deutsch, 2014, p. 216). Segundo Armstrong (1994, p. 306), a variância de krigagem não é adequada para calcular o intervalo de confiança como a média mais ou menos duas vezes o desvio padrão de krigagem. Na realidade, esta estatística não é uma medida de incerteza e sim da configuração espacial dos pontos de dados usados na krigagem (Journel e Rossi, 1989, p. 738).
Atualmente, essa estatística é usada como uma medida da distância média em relação aos pontos amostrais e, portanto, sem nenhuma relação com o teor estimado. Segundo Snowden (2001, p. 647), a variância de krigagem pode ser empregada como uma medida objetiva da confiança geoestatística de um dado bloco com relação à configuração dos dados.
Exemplo de variância de krigagem
Dentro de um domínio geológico, um mapa da variância de krigagem destaca a confiança relativa bloco a bloco e pode ser uma ferramenta para localização de sondagens adicionais (Snowden, 2001, p. 647). Um exemplo ilustrativo, da aplicação da variância de krigagem para classificação de recursos minerais, pode ser observado na Figura 3.
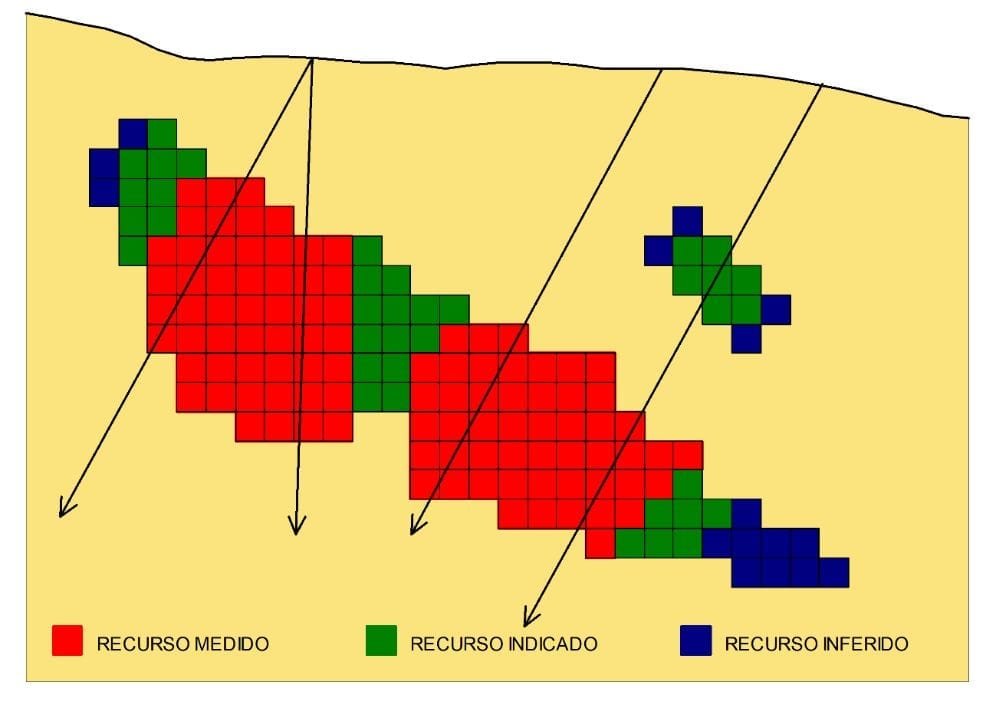
Cabe lembrar que a variância de krigagem é aplicada como limiar relativo, uma vez que os valores em si não têm nenhum significado físico ou geológico (Rossi e Deutsch, 2014, p. 218).
Espaçamento médio e densidade amostral
Os diferentes códigos para declaração de recursos minerais destacam a distribuição e configuração dos dados como um critério importante para confirmar a continuidade geológica e/ou de teores e, assim, classificar os recursos em medido, indicado e inferido, em ordem decrescente de confiança geológica (Mory e Deutsch, 2006, p. 309-1).
O espaçamento de dados tem sido usado como um critério geométrico para classificação, como uma medida da disponibilidade de dados e para avaliar os esquemas de amostragem (Pinto e Deutsch, 2018, p. 1).
Calculo do espaçamento médio
O espaçamento médio para malhas regulares pode ser calculado como a média das aberturas da malha nas direções X e Y (Mory e Deutsch, 2006, p. 309-3):
![]()
A densidade amostral é igual ao número de dados ou sondagens por hectare (Mory e Deutsch, 2006, p. 309-2):
![]()
As equações (1) e (2) podem ser relacionadas da seguinte forma (Mory e Deutsch, 2006, p. 309-3; Pinto, 2016, p. 13):

Como achar a densidade amostral
A Figura 4A ilustra uma malha de sondagens com aberturas iguais a 50 m na direção X e 25 m na direção Y, que resulta em um espaçamento médio igual a 37,50 m. Para a densidade amostral, considere-se o exemplo da Figura 4B, onde há 12 sondagens em uma área de 100×200 m2. Assim, a densidade amostral é igual a 6 furos por hectare.

O espaçamento médio para dados com distribuição irregular pode ser calculado da seguinte forma (Pinto e Deutsch, 2018, p. 2):
 Onde:
Onde:
![]()
Exemplo de cálculo do espaçamento médio
A Figura 5 apresenta um exemplo para o cálculo do espaçamento médio, conforme Pinto e Deutsch (2018, p.2). Nesta figura, a área engloba oito pontos (n=8), assim o raio médio é obtido como a média das distâncias entre o centro e o oitavo ponto e entre o centro e o nono ponto.
A distância para o oitavo ponto é igual a 42,85 m e para o nono ponto é 48,50 m, portanto o raio médio é 45,675 m. O espaçamento médio é igual a 28,62 m. A densidade amostral é 12,21 amostras ou furos por hectare.

Para dados 3D, o espaçamento médio pode ser calculado pela seguinte expressão (Pinto, 2016, p. 15; Pinto e Deutsch, 2018, p. 3):

Onde: V é o volume (m3) e c o intervalo de regularização em m.
Furos inclinados e furos verticais
A Figura 6 ilustra duas situações: furos inclinados (A) e furos verticais (B).
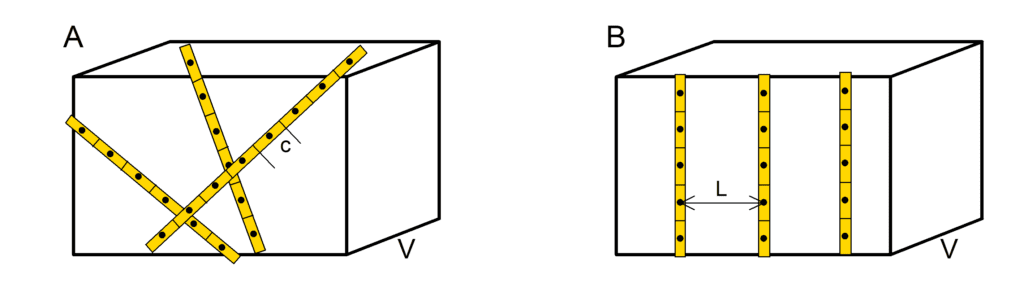
Para o caso de furos inclinados, tem-se 20 amostras em três sondagens. Considerando o intervalo de regularização c=10 m e o volume V=15625 m3, o espaçamento médio é igual a 8,84 m, conforme a equação (5). A densidade amostral, seguindo a equação (3), resulta em 33,64 amostras por hectare.
Mory e Deutsch (2006, p. 309-8) usam o critério geométrico (espaçamento médio e densidade amostral) combinado com critérios probabilísticos para a classificação de recursos minerais, para uma malha de sondagem hipotética.
Próximo artigo
No próximo artigo, o critério geométrico do espaçamento médio e o cálculo da densidade amostral serão ilustrados com um exemplo de aplicação em 2D.
Referências bibliográficas
Mory, D.F.M.; Deutsch, C.V. 2006. A program for robust calculation of drillhole spacing in three dimensions. Edmonton, CCG Report. P. 309-18.
Pinto, F.A.C. 2016. Advances in data spacing and uncertainty. Master thesis submitted to Department of Civil and Environmental Engineering, University of Alberta. 177p.
Pinto, F.A.C.; Deutsch, C.V. 2018. Calculation of high resolution data spacing models. In: Deutsch, J.L. (ed) Geostatistics lessons. Baixado em 25/10/2018 de: http://geostatisticslessons.com/lessons/dataspacing.
Rossi, M.; Deutsch, C.V. 2014. Mineral resource estimation. Dordrecht, Springer. 332p.
Sinclair, A.J.; Blackwell, G.H. 2002. Applied mineral inventory. New York, Cambridge University Press. 381p.
Snowden, D.V. 2001. Practical interpretation of mineral resource and ore reserve classification guidelines. In: Mineral Resources and Ore reserve Estimation – The AusIMM Guide to a Good Practice (Ed. A.C. Edwards) p. 643-652. Melbourne, The Australasian Institute of Mining and Metallurgy.





