A Incerteza na Estimativa por Krigagem Ordinária

Variância de krigagem

A geoestatística teve uma grande aceitação ao proporcionar uma medida de incerteza associada à estimativa por krigagem ordinária, por meio da variância de krigagem. Esta aproximação foi utilizada há quase três décadas até a publicação de Journel e Rossi (1989).

Nesta ocasião, os autores afirmaram que a variância de krigagem deveria ser empregada apenas como uma medida da configuração espacial dos pontos de dados considerados na estimativa de uma localização não amostrada.

Ilustrando a variância

Para ilustrar esse problema, vamos considerar a Figura 1 em que dois blocos em diferentes localizações precisam ser estimados. Devido à configuração dos pontos de dados, as estimativas são exatamente iguais, mas a incerteza não. No caso do bloco A, a incerteza é baixa, enquanto para o bloco B a incerteza é muito alta.

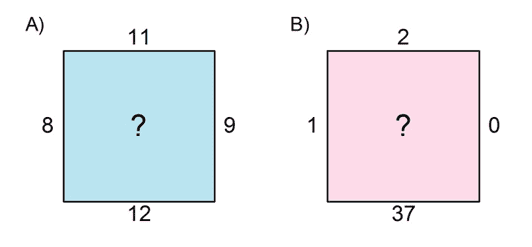
Figura 1: Estimativa de blocos com a mesma configuração
espacial dos pontos de dados (Segundo Armstrong, 1994).

A variância de interpolação (Yamamoto, 2000), por outro lado, considera não somente a localização dos pontos de dados, como também a dispersão local, por meio da seguinte equação:

Quais são as propriedades da variância de krigagem?

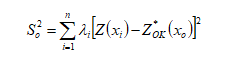
Segundo Yamamoto (2000, p. 492):

• garante a exatidão, pois se um ponto de dado coincide com o ponto a ser interpolado, a variância de interpolação será igual a zero;
• aumenta com a dispersão dos valores próximos utilizados na interpolação;
• usa indiretamente a informação estrutural por meio dos pesos da krigagem ordinária.

Os mapas da variância

Quando os pontos de dados estão regularmente distribuídos sobre a área de estudo, o mapa da variância de krigagem irá refletir baixa variância sobre os pontos e alta entre os pontos de dados, independente da dispersão dos pontos de dados.

Esse é o caso mostrado na Figura 2, onde a variância de krigagem mostra um padrão regular tal como a distribuição dos pontos de dados. Entretanto, a variância de interpolação apresenta um padrão que independe da geometria da distribuição dos pontos de dados, mas sobretudo da variabilidade espacial.

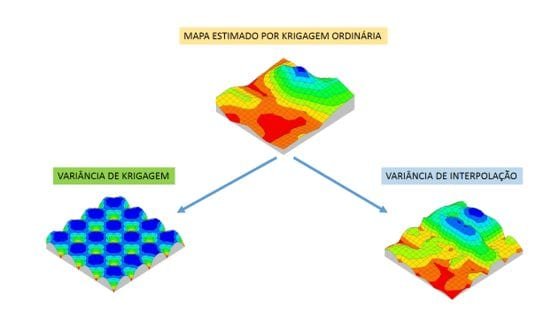
Figura 2: Variância de krigagem e variância de interpolação como
medidas de incerteza associadas à estimativa por krigagem ordinária
de um conjunto de dados com distribuição regular.

Referências

Armstrong, M., 1994, Is research in mining geostats as dead as a dodo?: in Dimitrakopoulos, R., ed., Geostatistics for the next century: Kluwer Academic, Dordrecht, Netherlands, p. 303–312.

Journel, A. G., and Rossi, M. E., 1989, When do we need a trend model in kriging?: Math. Geology, v. 21, no. 7, p. 715–739.

Yamamoto, J.K. 2000, An alternative measure of the reliability of ordinary kriging estimates. Math. Geol., v. 32, p. 489-509.

O artigo foi útil para você? Compartilhe!