“Geostatistical Ore Reserve Estimation” – Resenha de obra de M. David
A obra
David publica um livro denominado “Estimativa Geoestatística de Reservas Minerais” (“Geostatistical Ore Reserve Estimation“, 1977) que representa uma importante contribuição à divulgação da geoestatística. Esta obra ainda permanece como uma referência para consulta. Trata-se de um texto acompanhado de ilustrações que ajudam no entendimento das técnicas e conceitos matemáticos empregados em geoestatística.
Capítulos da obra
Este livro é dividido em 13 capítulos:
- Teoria estatística elementar e aplicações
- Contribuição das distribuições para os problemas de reservas minerais
- O que é o cálculo de reservas?
- O que é um variograma
- Base teórica da aproximação: a Teoria das variáveis regionalizadas
- A prática da modelagem de variogramas
- Cálculo efetivo de variâncias de blocos
- Cálculo das variâncias de estimativa: problemas de precisão
- Otimização da estimativa de teores: krigagem
- Prática da krigagem
- Curvas teor-tonelagem, seleção minério-rejeito e problemas de planejamento
- Modelagem de corpos de minério
- Problemas estatísticos na preparação de amostras.
Capítulo 1
No capítulo 1, David (1977, p. 4) afirma que a distribuição de probabilidades pode ser obtida a partir da distribuição de frequências pela simples divisão de cada uma das frequências por n que é o número total de observações. Dentre as diversas distribuições estatísticas descritas, David (1977, p. 23) menciona a distribuição de Poisson, que modela a distribuição aleatória de unidades de interesse dentro de um dado volume.
Capítulo 2
No Capítulo 2, o autor aborda a questão do uso de distribuições de teores para a construção de curvas teor-tonelagem, onde diferentes teores de corte são considerados e diferentes tonelagens são computadas, cada uma com o teor médio associado (David, 1977, p. 39).
Capítulo 3
O Capítulo 3 trata da questão de avaliação de reservas minerais, conforme: sabe-se os teores reais localizados em algumas amostras e se deseja saber o teor de um bloco maior ou mesmo da mina inteira; assim, a solução natural conhecendo os poucos valores de teores (t1, t2, …, tn) seria manipulá-los a fim de se ter uma combinação desses teores que será considerado como o teor real do bloco em estudo (David, 1977, p. 52). Fazendo essas manipulações, quaisquer sejam essas, implicam em dois conceitos básicos: erro de extensão (estender o teor de uma amostra para um bloco de dimensão maior) e do erro de estimativa (que ocorre devido ao fato que amostras e blocos não serem estritamente equivalentes), segundo David (1977, p. 53).
Capítulo 4
O Capítulo 4 introduz o cálculo do variograma, que mede a similaridade ou dissimilaridade que existe entre o teor de um ponto com o teor em outro ponto (David, 1977, p. 73). Destaca-se ainda o uso e aplicação da variável acumulação (produto do teor pela espessura mineralizada) em que os variogramas da espessura e acumulação são proporcionais (Figura 1).

Capítulo 5
No Capítulo 5, o autor descreve a Teoria das Variáveis Regionalizadas. Faz ainda uma observação sobre o fator 2 na definição da função variograma como 2ϒ(h), que por questão de simplicidade pode se usar ϒ(h) como variograma, ao invés de se chamar de semivariograma (David, 1977, p. 94). Segundo David (1977, p. 99), o efeito pepita pode ser considerado como uma variância de componente totalmente aleatória superposta à variável regionalizada.
Capítulo 6
O Capítulo 6 trata da prática da modelagem de variogramas, onde se destaca a correção de anisotropia aparente por meio da obtenção de variogramas relativos (David, 1977, p. 172-173), como se ilustra na Figura 2. Segundo David (1977, p. 172), variogramas relativos são extremamente úteis, pois conforme essa figura, três variogramas muito diferentes correspondentes a três diferentes direções são na verdade absolutamente iguais, uma vez divididos pela média local.

Capítulo 7
O Capítulo 7 é dedicado ao cálculo efetivo de variâncias dos blocos. O problema surge quando se precisa saber a variância dos blocos de um determinado tamanho para fazer a previsão da variabilidade de uma massa minerada (David, 1977, p. 176). Esse autor introduz o conceito da função F que permite calcular o valor médio do variograma entre dois pontos dentro do bloco V:
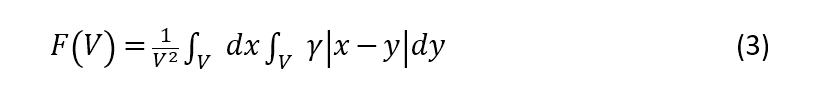
Devido à dificuldade de se calcular essas integrais, emprega-se ábacos para determinação dos valores da função F (David, 1977, p. 176).
Capítulo 8
O Capítulo 8 trata dos problemas de precisão associados ao cálculo de variâncias de estimativa. Trata-se em calcular a variância de estimativa do teor de um blocoavaliado por um número de amostras próximas. A variância de estimativa pode ser calculada como (David, 1977, p. 192):

Onde V é o volume do bloco e as N amostras xi.
Na prática, o cálculo da integral é realizado por uma soma discreta de pontos, localizados regularmente dentro do bloco V, como se faz nos atuais programas para krigagem ordinária. David (1977, p. 193-195) proporciona o código de um programa de computador em Fortran IV para o cálculo da variância de estimativa de um bloco. É interessante ilustrar as extensões mais comuns envolvidas no cálculo dos teores dos blocos, conforme a Figura 5.
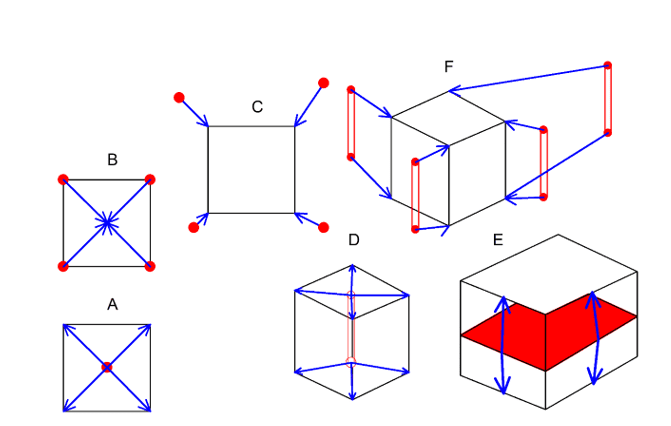
É importante ressaltar que ao se fazer a atribuição de teores de pontos amostrados para blocos, sempre haverá uma incerteza, devido tanto à natureza estocástica da variável geológica, bem como pelo desconhecimento devido à amostragem insuficiente.
Capítulo 9
O capítulo 9 intitulado “Otimização da estimativa de teores: krigagem” trata da questão da krigagem propriamente dita, onde o autor desenvolve as equações de krigagem, bem como uma listagem do programa Krige2 para o cálculo da krigagem de bloco (David, 1977, p. 261-265). Além disso, o autor apresenta a técnica da krigagem universal para dados contendo uma tendência.
Capítulo 10
O Capítulo 10 ainda se dedica ao tema da krigagem, mas se refere aos problemas práticos envolvidos, tais como: pesquisa dos vizinhos próximos, cálculo das covariâncias, resolução do sistema de equações, definição do plano de krigagem e a questão das malhas de amostragem, se regular ou irregular (David, 1977, p. 275-300).
Capítulo 11
No capítulo 11, o autor descreve as curvas teor-tonelagem, seleção de minério-rejeito e problemas de planejamento, os quais são abordados e ilustrados com estudos de casos reais (David, 1977, p. 301-320).
Capítulo 12
O Capítulo 12 intitulado modelagem do corpo de minério diz respeito ao problema dos valores médios dos teores e a flutuação dos teores de minério. Segundo David, (1977, p. 321), o primeiro problema pode ser resolvido pela krigagem, enquanto o segundo por meio da simulação de teores dos blocos. Assim, introduz-se o assunto da simulação que permite inferir as flutuações das predições, por meio das diversas realizações.
Capítulo 13
Finalmente, no capítulo 13, o autor trata dos problemas estatísticos relacionados à preparação de amostras, em que os erros em geral são pequenos, mas podem ser grandes e não negligenciáveis.
Referências:
David, M. 1977. Geostatistical Ore Reserve Estimation – Developments in Geomathematics 2. Ecole Polytechnique, Université de Montréal, Montréal, Quebec, Canada.
Leia os artigos anteriores da nossa série de resenhas:
Interessado em Geoestatística? Nossos cursos podem impulsionar seu conhecimento e destacar você:






