Retrospectiva da Geoestatística VII: Monografia de J.-M. Rendu (1978)

Resenha: Monografia de Jean Michel Rendu – “An Introduction to Geostatistical Methods of Mineral Evaluation”)

Rendu (1978) publica sua monografia intitulada “Uma Introdução aos Métodos Geoestatísticos de Avaliação Mineral” (“An Introduction to Geostatistical Methods of Mineral Evaluation”), que foi patrocinada pelo Instituto Sul Africano de Minas e Metalurgia.

 

Capítulos

Essa monografia é subdividida em 12 capítulos:

1. Introdução;
2. Estatística clássica, distribuições aleatórias e teorias normal e lognormal;
3. Estatística espacial, covariograma e semivariograma, definições e cálculos;
4. Representação matemática dos semivariograma e covariogramas;
5. Regularização;
6. Cálculo de γ e σ : funções auxiliares e gráficos;
7. Variância de dispersão e relação teor-tonelagem;
8. Variância de extensão e variância de estimativa;
9. Avaliação ótima e krigagem;
10. Avaliação ótima usando informação histórica: um estudo de caso;
11. Krigagem aleatória;
12. Krigagem universal.

 

Este texto é de grande utilidade para o melhor entendimento da origem da geoestatística, pois contém explicações detalhadas como foram desenvolvidas as técnicas até hoje utilizadas.

O Capítulo 2 apresenta uma revisão dos conceitos estatísticos empregados na avaliação de recursos minerais.

No Capítulo 3, o autor trata dos conceitos de estatística espacial para derivar as funções covariograma e semivariograma.

No Capítulo 4, Rendu (1978, p. 18-21) descreve os modelos matemáticos para representação dos semivariogramas.

 

O que é Regularização

O Capítulo 5, intitulado “Regularização”, deriva a relação fundamental da regularização. Ou seja, onde se deseja determinar o semivariograma médio em volumes ou áreas, a partir do semivariograma pontual (Rendu, 1978, p. 22):

Onde

 

 

é o valor médio do semivariograma pontual entre dois pontos w e w_+h;

é o valor médio entre quaisquer dois pontos na mesma amostra w. Além disso, apresenta algumas curiosidades como, por exemplo, o cálculo de variogramas experimentais para dados com distribuição irregular.

Rendu (1978, p. 26-27) aplica a regularização de dados aleatórios (Figura 1),. Isto é, onde uma malha regular é superposta aos dados e os pontos de dados dentro de cada célula são usados para o cálculo da média aritmética simples. Em seguida, a malha regular assim obtida era aplicada para o cálculo de variogramas experimentais com base no algoritmo disponível para dados distribuídos regularmente.

 

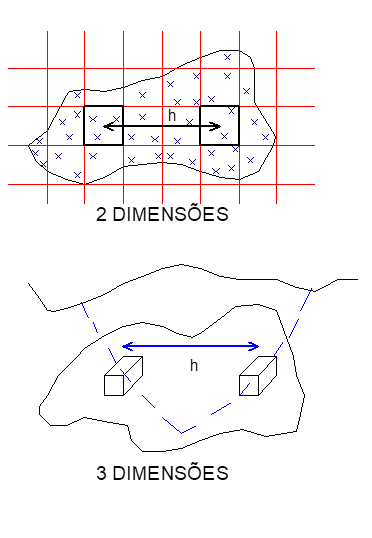
O Cálculo de γ e σ

O Capítulo 6 mostra o cálculo de γ e σ, por meio de aproximação numérica, bem como por meio das funções auxiliares e gráficos. Atualmente, aplica-se a aproximação numérica fazendo a discretização da área ou volume a ser estimado.

 

A Prova da Relação Fundamental 

No Capítulo 7, destaca-se a prova da relação fundamental (Rendu, 1978, p. 48):

Onde  σ²(w^o em w) é a variância do valor de um ponto em um bloco w. Para tanto, Rendu (1978, p. 48) considera um bloco w no corpo de minério Ω, que é composto por n pontos amostrais w^o localizados nos pontos z_i com valores {x_i, i=1,n}. Segundo esse autor, a variância de dispersão de w^o em w é a variância esperada de x em w, quando w toma todas as posições em Ω. Assim, a média amostral é:

E a variância de w^o em um bloco w é (Rendu, 1978, p. 48):

 

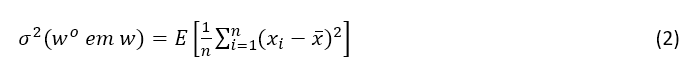
Segundo esse autor, o lado direito da expressão (2), pode ser escrito como:

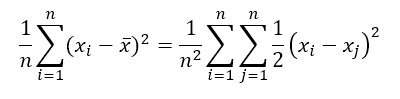
E, portanto:

Como se pode observar, o desenvolvimento é feito exclusivamente com base nas estatísticas média e variância.

 

A Variância de Extensão

O Capítulo 8 mostra como se pode calcular a variância de extensão, a partir das estatísticas amostrais. Para isso, considere-se o conjunto amostral ws composto por p pontos com valores {x_j, j=1,p} e o bloco W com q valores {x_k, k=1,q} (Rendu, 1978, p. 54):

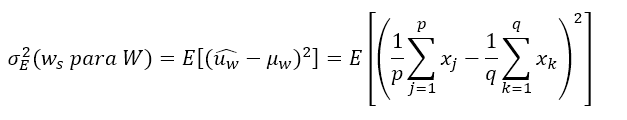
Em termos da função variograma, tem-se:

Rendu aborda a Krigagem

O Capítulo 9 se intitula “Avaliação ótima e krigagem” apresenta a teoria da krigagem, onde o autor discute várias situações acompanhadas do desenvolvimento teórico.

No Capítulo 10, segundo Rendu (1978, p. 65), em muitas situações práticas o cálculo do semivariograma não é necessário, como, por exemplo, o caso de uma grande seção minerada em que foi intensamente amostrada e que não apresenta tendência. Assim, segundo esse autor, os geólogos esperam que as áreas não mineradas sejam similares às mineradas.

O Capítulo 11 trata da questão da amostragem não regular, onde a solução encaminhada para o problema se denomina krigagem aleatória.

Por fim, o Capítulo 12 apresenta a krigagem universal que, segundo Rendu (1978, p. 76), tem dificuldades práticas: escolha da função de tendência e a estimativa do covariograma residual.

 

 

 

 

 

 

Referências:

Rendu, J.-M. An Introduction to Geostatistical Methods of Mineral Evaluation. Johannesburgo, Institute of Mining and Metallurgy. 84p.

Retrospectiva da Geoestatística VI: Geoestatística lognormal-de Wijsiana, Krige (1978)

 

 

 

 

 

Gosta de Geoestatística? Aprenda mais sobre seus conceitos: