Introdução a Análise Composicional- GEOKRIGAGEM

Análise Composicional Introdução

Definição de dados composicionais

Dados composicionais consistem em vetores cujas componentes são proporções ou porcentagens de algum total. Sua peculiaridade é que sua soma está restrita a uma constante: 1 para proporções, 100 para porcentagens ou possivelmente outra constante c como, por exemplo, em partes por milhão (ppm) em composições de traços de elementos.

Lamentavelmente uma olhada superficial para estes dados dá a impressão de serem vetores com números reais. Consequentemente, nas últimas décadas, todos os métodos estatísticos concebidos para dados sem restrições foram empregados em dados composicionais. Isto ocorre apesar dos profissionais estarem conscientes – ou deverem estar conscientes – de que o espaço amostral para vetores composicionais é radicalmente diferente do espaço euclidiano real associado a dados sem restrições.

Várias advertências foram feitas, algumas tão antigas como em 1897, por Karl Pearson, sobre correlações espúrias em dados composicionais e, muito tempo depois, em 1960, pelo geólogo Felix Chayes.

Inicialmente as tentativas para superar os problemas se limitaram a ver o que estava dando errado quando se aplicavam diretamente as técnicas de análise multivariada a dados composicionais. Mas foi somente a partir dos trabalhos de John Aitchison que uma nova teoria matemática foi desenvolvida para tratar adequadamente dos problemas relacionados a dados composicionais.

A teoria

O seu ponto de partida é o reconhecimento do espaço amostral adequado para dados composicionais – um simplex D-1 dimensional é a envoltória convexa de um conjunto de pontos D dimensionais. Na figura, vemos um simplex de dimensão 2, representando um conjunto de pontos tri-dimensionais, correspondendo às composições de Bi, Hf e Tl.

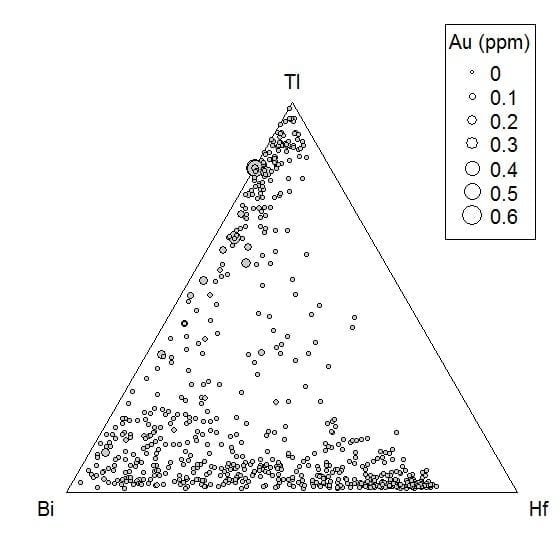
Na teoria composicional, as coordenadas desses pontos serão sempre positivas. Casos de zeros serão tratados como elementos faltantes ou abaixo do limite de detecção, SD = {X; xi>0,i=1,2,…,D; Σ xi=c}.

Princípios da Análise Composicional

Usualmente trabalha-se com o conceito de subcomposição, que é uma composição com apenas parte dos componentes. Na realidade, a maioria das composições é uma subcomposição já que dificilmente analisamos todos os possíveis componentes de uma amostra. Por esse motivo, há alguns princípios que a teoria deve observar:

Invariância por escala

As composições [12,3,4]; [2400,600,800]; [12/17,3/17,4/17] são equivalentes.

Invariância por perturbação

(mudança de unidades) As composições [0.5211, 0.2394, 0.2934] porcentagem em 100g de massa e [0.4, 0.26, 0.34] Kj/g são equivalentes.

Coerência subcomposicional

Distâncias entre duas composições serão maiores do que as distâncias entres as respectivas subcomposições. Além disso, a dispersão total entre um conjunto de dados composicionais é maior do que a dispersão para um conjunto das respectivas subcomposições.