Interpolação – Parte 2

Dando continuidade à série de artigos sobre interpolação, vamos apresentar o conceito da fronteira convexa e a localização de pontos em relação a mesma. Muitos programas de interpolação de dados simplesmente não oferecem a alternativa para determinação da fronteira convexa.

Trata-se de uma etapa importante na análise de dados geoespaciais, pois a interpolação fora do domínio da amostragem pode criar variações espaciais completamente artificiais, sem nenhuma relação com os dados amostrais.

Uma vez definida a fronteira convexa, os seus limites devem ser usados para determinar os pontos da malha regular que podem ser interpolados. Essa verificação é feita se aplicando algoritmos de localização de um ponto em relação a um polígono.

2 – Fronteira convexa

Por definição, a fronteira convexa é o polígono convexo de área mínima que engloba os pontos de dados. A interpolação deve ser feita somente dentro desse domínio amostral, pois fora do mesmo é extrapolação. A amostragem pode ser orientada conforme a estrutura geológica ou traço da mineralização e, dessa forma, nem todo o espaço a ser mapeado contém pontos de dados.

A superposição da fronteira convexa é necessária para se evitar extrapolações, conforme se pode visualizar na Figura 3. De acordo com esta figura, existem quadrantes vazios que não têm significado algum quando extrapolado.

A Figura 4 ilustra um conjunto de pontos de dados com a superposição da fronteira convexa.

3 – Verificação dos Pontos do Grid em Relação à Fronteira Convexa

Cada ponto da malha regular é verificado se está dentro ou fora da fronteira convexa. Existem vários algoritmos, mas o mais simples é aquele publicado por Anderson (1976, p. 105-106), que consiste em contar as intersecções da reta traçada à direita cortando a fronteira convexa. Se o número de intersecções for par, então o ponto está fora; se for ímpar, o ponto está dentro (Figura 5).

Figura 5: Ilustração do algoritmo de Anderson (1976, p. 105-106) de contagem de intersecções: A) número ímpar, ponto dentro; B) número par, ponto fora (Yamamoto, 2020, p. 145).

A malha regular é conveniente para analisar a distribuição espacial da variável, pois os valores são representativos de áreas (Figura 2B) ou volumes constantes. Outra razão para o cálculo de malhas regulares está justamente na visualização dos resultados, seja por meio de mapa imagem ou mapa de isovalores (Figura 2A), bem como a representação em perspectiva da superfície.

4 – Pesquisa dos vizinhos próximos

Os métodos locais precisam identificar a vizinhança próxima do ponto a ser interpolado, conforme algum critério. O importante é que essa localização seja rápida, pois é inviável processar todos os pontos de dados, calcular a distância para o ponto a ser interpolado e selecionar os mais próximos.

Um algoritmo eficiente para esta localização rápida, denomina-se pesquisa por superblocos (Deutsch e Journel, 1992, p. 31-32). Basicamente, os pontos de dados são classificados conforme o modelo de blocos definido.

Dessa maneira, dado um bloco a ser interpolado, apenas os blocos da sua vizinhança são pesquisados, evitando dessa maneira a pesquisa de outros pontos distantes do objetivo.

Além disso, há necessidade também de se estabelecer um critério para seleção dos n pontos vizinhos. Há diversos critérios citados por Harbaugh et al. (1977, p. 108-110), como, por exemplo, vizinhos mais próximos, quadrantes e octantes.

A título de comparação, a Figura 6 ilustra os processos de busca pelos vizinhos mais próximos e por quadrantes (Harbaugh et al., 1977, p. 108-109).

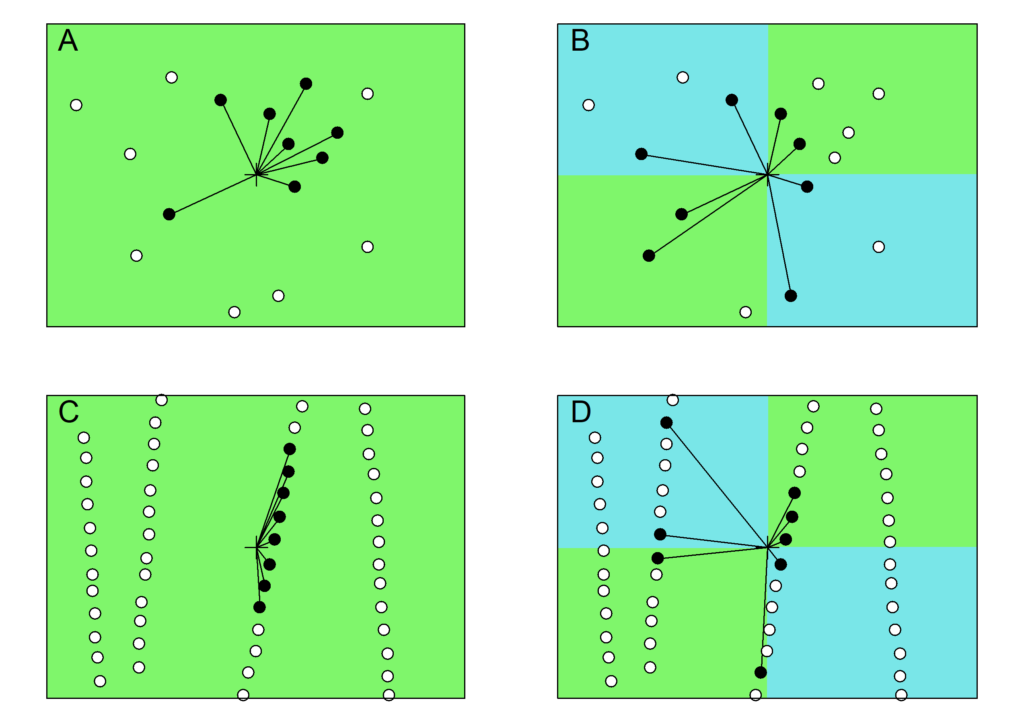
Nessa figura, há dois arranjos de dados um irregular e outro semirregular. Na pesquisa pelos vizinhos mais próximos (Figuras 6A e 6C), verifica-se que a amostragem não é representativa do conjunto de dados da vizinhança. Por outro lado, quando se faz a pesquisa por quadrantes (Figuras 6B e 6D), os pontos localizados garantem uma boa representação espacial.

Referências Bibliográficas

Anderson, K.R. 1976. Simple algorithm for positioning a point close to a boundary (Letters to the Editor). Math. Geology, v. 8, p. 105-106.

Deutsch, C.V.; Journel, A.G. 1992. GSLIB – Geostatistical software library and user’s guide. New York, Oxford University Press. 340p.

Harbaugh, J.W.; Doveton, J.H.; Davis, J.C. 1977. Probability methods in oil exploration. New York, John Wiley & Sons. 269p.

Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 308p.