Classificação de Recursos e Reservas Minerais – Parte 3: Incertezas da Krigagem Ordinária

Estimativa de Recursos Minerais

Série de artigos: Classificação de Recursos Minerais

Classificação de Recursos e Reservas Minerais Parte 1: Parâmetros de Classificação (CBRR)

Classificação de Recursos e Reservas Minerais Parte 2: Continuidade Geológica e de Teores

 

Classificação de Recursos e Reservas Minerais – Parte 3: Incertezas da Krigagem Ordinária

Estimativa de recursos minerais

A estimativa de recursos minerais é feita por meio da krigagem ordinária, que é o método padrão adotado na indústria mineral. Após a estimativa, deve-se fazer a classificação dos recursos minerais, com base em algum critério definido pela pessoa competente.

A principal premissa para a classificação de recursos minerais está fundamentada na confiança dos dados amostrais em relação ao bloco estimado. Deve-se levar em consideração que a estimativa é sempre feita a partir das amostras coletadas ao longo das sondagens. A maioria dos blocos de um modelo tridimensional de blocos será estimada com base nas amostras de sondagens vizinhas (Figura 1). A estimativa dos recursos minerais do depósito em estudo é obtida se somando os blocos individuais do modelo tridimensional.

 

Erros de amostragem são  ruins?

Segundo Sinclair e Blackwell (2002, p. 27-28), as amostras reduzidas para análises dos teores constituem apenas um milionésimo do depósito e, consequentemente, erros são esperados. Assim, os erros de estimativa podem ser vistos como erros de extensão, ou seja, erros cometidos na extensão de teores das amostras para um volume muito maior de rocha (Sinclair e Blackwell, 2002, p. 2). As extensões mais comuns podem ser observadas na Figura 2 (David, 1977, p. 203). Como se pode verificar, os erros de estimativa, pela extensão de teores de amostras vizinhas para estimativa do bloco, são inevitáveis.

Incerteza geológica na classificação de recursos minerais

Como apresentado no artigo anterior, os dois critérios fundamentais para a classificação de recursos minerais são: continuidade geológica e continuidade de teores. Assim, idealmente os esquemas para classificação deveriam considerar a incerteza combinada da interpretação geológica e da interpolação de teores (erro de extensão). Entretanto, é muito difícil quantificar a incerteza geológica pois, ela existe ou não. Por outro lado, a incerteza associada à estimativa de teores pode ser avaliada por meio da variância de krigagem ou da variância de interpolação. Desta forma, vamos revisar os conceitos referentes às aproximações usadas para modelagem da incerteza.

 

Variância da krigagem

O que é variância de krigagem?

A variância de krigagem é apenas uma medida da configuração espacial dos pontos de dados usados na estimativa.

Na verdade, a variância de krigagem é um índice de configuração dos dados baseado no modelo do variograma, mas independente dos valores dos dados e, portanto, não é uma medida de exatidão local (Journel e Rossi, 1989, p. 738).

Yamamoto e Landim (2013, p. 76-77) ilustram estimativas feitas em diferentes localizações e diferentes pontos de dados, que resultam nas mesmas variâncias de krigagem.

A variância da krigagem para a classificação de recursos minerais

A variância de krigagem foi usada inicialmente para classificação de recursos minerais (Rossi e Deutsch, 2014, p. 216). Armstrong (1994, p. 306) condena o uso da variância de krigagem para fins de classificação de recursos minerais. Essa autora usa o exemplo ilustrado na Figura 3, onde os dois blocos apresentam a mesma variância de krigagem. Como se pode verificar nesta figura, o bloco B apresenta uma incerteza muito maior devido à maior dispersão dos pontos de dados. Apesar dos contras em relação à variância de krigagem, como uma medida da configuração espacial dos dados, pode ser usada para fazer a medida indireta da distância em relação aos pontos mais próximos.

 

Variância de interpolação

A variância de interpolação foi proposta por Yamamoto (2000, p. 491-493), como uma medida alternativa da confiabilidade das estimativas da krigagem ordinária. Essa estatística apresenta as seguintes propriedades (Yamamoto, 2000, p. 492):

• Garante a exatidão: de fato, se um ponto de dado coincide com o ponto a ser estimado, o peso do dado é igual a um com todos os demais iguais a zero, portanto a variância de interpolação será igual a zero;
• Aumenta com a dispersão dos pontos de dados usados na krigagem ordinária;
• Usa indiretamente a distância estrutural do variograma, por meio do peso da krigagem ordinária, sendo que o dado mais influente recebe o maior peso.

Diferença entre variância de krigagem e variância de interpolação

Ao contrário da variância de krigagem, esta alternativa oferece a possibilidade de se medir a dispersão real dos pontos de dados em relação à estimativa feita por krigagem ordinária. Nesse sentido, ela pode ser usada para calcular o intervalo de confiança da estimativa, bem como para derivar outras estatísticas de interesse.

Potencial para pesquisa

Entretanto, não há ainda nenhuma proposta efetiva para o uso da variância de interpolação para fins de classificação de recursos minerais. Assim, esse assunto deve ser objeto de pesquisa futura visando a sua utilização para a composição de incerteza juntamente com a incerteza geológica.

 

Efeito proporcional

O que é o efeito proporcional

O efeito proporcional é uma condição na qual a variância do erro é proporcional à alguma função da média local dos dados (Olea, 1991). Na realidade, o efeito proporcional é uma propriedade de distribuições lognormais, ou seja, para distribuições de metais raros (ouro, prata, cobre, tungstênio etc.).

A Figura 4 ilustra os resultados de uma krigagem ordinária para dados com distribuição lognormal, onde o histograma dos teores médios apresenta uma assimetria positiva (Figura 4A). O efeito proporcional pode ser observado no diagrama de dispersão (Figura 4B) do desvio padrão de interpolação em função do teor médio do bloco.

Nesse caso, como o desvio padrão de interpolação aumenta com o teor, não se pode usar diretamente a medida de incerteza para fins de classificação de recursos minerais. Observe-se que alta incerteza não significa menor confiança na estimativa, pois ela está associada a um alto teor. Assim, pode-se usar a estatística adimensional denominado coeficiente de variação (CV), que resulta da divisão do desvio padrão pela média. Esta estatística só é possível obter a partir do desvio padrão de interpolação. A distribuição dos valores do coeficiente de variação está representada no histograma da Figura 5, conforme os dados apresentados na Figura 4B.

Distribuição de frequências para classificar os recursos minerais

Para fins de classificação de recursos minerais com base no coeficiente de variação, a distribuição poderá ser dividida em intervalos de valores crescentes, que correspondam aos recursos minerais medidos, indicados e inferidos. Apenas a título de ilustração para o exemplo, pode-se usar os seguintes intervalos:

 

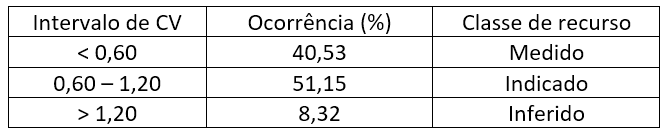
Evidentemente, os intervalos de CV deverão ser definidos para cada tipo de depósito mineral e de acordo com a distribuição de frequências da variável em estudo.

Esse assunto será retomado futuramente, quando se discutir os métodos de classificação de recursos minerais.

Comparação entre variância de krigagem e variância de interpolação

Quando o ponto estimado está sobre um ponto de dado, tanto a variância de krigagem como a variância de interpolação são iguais a zero. Entretanto, quando o ponto estimado não coincide com um ponto amostral, a incerteza aumenta não apenas com a distância, mas também com a dispersão dos valores dos pontos de dados.

A Figura 6 foi obtida a partir de uma malha regular de 5 por 5 pontos de dados. Como se pode verificar, a variância de krigagem reflete exatamente a malha dos pontos amostrais, enquanto a variância de interpolação aumenta com a dispersão dos pontos, conforme o modelo da variável krigada.

 

              No próximo artigo, abordaremos a questão da continuidade geológica, por meio do modelo geológico. Como visto anteriormente, a continuidade geológica é o fator chave na classificação de recursos minerais.

Referências bibliográficas

Armstrong, M. 1994. Is research in mining as dead as a dodo? In: Dimitrakopoulos, R. (Ed.) Geostatistics for the next century. Dordrecht, Springer. p. 303-312.

David, M. 1977. Geostatistical ore reserve estimation. Amsterdam, Elsevier. 364p.

Journel, A.G.; Rossi, M. 1989. When do we need a trend model in kriging? Math. Geology, v. 21, p. 715-739.

Olea, R.A. 1991. Geostatistical glossary and multilingual dictionary. New York, Oxford University Press. 177p.

Yamamoto. J.K. 2000. An alternative measure of the reliability of ordinary kriging estimates. Math. Geol., v. 32, p. 489-509.

Yamamoto, J.K.; Landim, P.M.B. 2013. Geoestatística – fundamentos e aplicações. São Paulo, Oficina de Textos. 215p.