Estatísticas descritivas: tendência central e dispersão

O que são as estatísticas descritivas?

Nos artigos anteriores, vimos como sumariar a informação disponível, por meio da distribuição de frequências e suas representações gráficas (histograma e curva acumulativa). Na realidade, as representações gráficas permitem fazer a caracterização qualitativa da distribuição de frequências. A descrição quantitativa das distribuições de frequência pode ser feita por meio das estatísticas descritivas básicas.

As estatísticas amostrais se referem à sua distribuição de frequências. Por outro lado, os parâmetros se referem à população, quando conhecida. As estatísticas descritivas podem ser agrupadas em: medidas de tendência central, medidas de dispersão e medidas de forma.

As medidas de tendência central são: média, mediana e moda. Estas estatísticas indicam os valores mais prováveis da distribuição de frequências. As estatísticas de tendência central coincidem para uma distribuição simétrica. Caso contrário, a média se desloca em relação à mediana. Na distribuição com assimetria positiva, a média é maior que a mediana. A média menor que a mediana ocorre para distribuição com assimetria negativa.

A média de uma variável aleatória X pode ser calculada como:

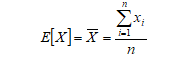 (1)

Por definição, a moda é o valor mais frequente da distribuição, que pode ser obtido a partir da classe de maior frequência do histograma. A mediana é o valor correspondente a 50% da distribuição de frequências. A Figura 3 ilustra graficamente as medidas de tendência central associadas à distribuição de frequências da variável Zgauss.

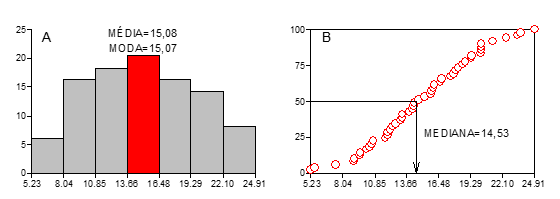
Figura 1: Estatísticas de tendência central para a distribuição de
frequências da variável Zgauss: média e moda (A) e mediana (B).

Como se pode verificar na Figura 3, a média e moda são praticamente iguais. A mediana é menor que a média, confirmando uma pequena assimetria da distribuição de frequências.

As medidas de dispersão em torno da média são dadas pela variância, pelo desvio padrão, coeficiente de variação e pela amplitude interquartil. A variância pode ser calculada como:

 (2)

O desvio padrão é simplesmente a raiz quadrada da variância:

 (3)

A variância é calculada como a média do momento de segunda ordem (em torno da média) como mostra a equação acima. Pode-se mostrar graficamente representando os momentos de segunda ordem como barras proporcionais e daí a média dessas barras resultando na variância (Figura 4).

Figura 2: Representação dos momentos de 2ª ordem como barras proporcionais e da variância.

Na verdade, a média como se pode observar na Figura 4 é o valor que minimiza a variância, ou seja, qualquer outro valor resultará em variância maior.

Continuaremos com este assunto. Aguarde!

Quer aprender mais sobre estatísticas descritivas?

Confira aqui nosso curso de Geoestatística: Fundamentos e Aplicações e aprenda muito mais desse universo.