O que é a distribuição uniforme?

O conceito da distribuição uniforme é importante em problemas de simulação estocástica, onde um valor entre zero e um é sorteado aleatoriamente para amostragem de uma função de distribuição acumulada condicional (método de Monte Carlo). Mas, ela é usada também para um tipo especial de transformação de dados denominada transformada do escore uniforme (Yamamoto, 2010).

Função densidade de probabilidade uniforme

A função densidade de probabilidade de uma distribuição uniforme no intervalo [a,b] é dada por (Yang, 2008):

Onde a e b são os parâmetros da distribuição uniforme. Fora do intervalo, a função densidade de probabilidade é zero.

A função de densidade acumulada é (Jensen et al. 2000):

A esperança matemática é igual a (Yang, 2008):

Devido à simetria da distribuição, a mediana é igual à esperança matemática e a moda por causa da uniformidade pode ser qualquer valor entre (a,b).

A variância, segundo Yang (2008), é igual a:

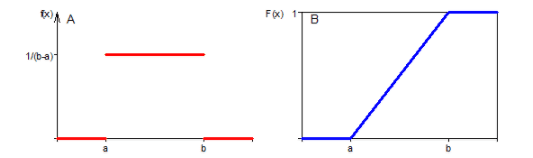
A função densidade de probabilidade da distribuição uniforme e a sua função densidade acumulada encontram-se ilustradas na Figura 7.

Figura 7: Função densidade de probabilidade da distribuição uniforme (A) e função densidade acumulada (B).

Outro modelo de distribuição de probabilidades comumente utilizado em geoestatística é a distribuição triangular, que tem aplicação quando se conhece um ponto dentro do intervalo de valores possíveis. A distribuição triangular será tema do nosso próximo artigo.

Referências:

Jensen, J.L.; Lake, L.W.; Corbett, P.W.M.; Goggin, D.J. 2000. Statistics for petroleum engineers and geoscientists. Amsterdam, Elsevier. 341p.

Yamamoto, J.K. 2010. Backtransforming rank order kriging estimates. Geologia USP. Série Científica, v. 10, p. 101-115.

Yang, X. 2008. Mathematical modelling for Earth Sciencesd. Edinburgh, Dunedin Academic Press. 310p.