Correção direta do Efeito de Suavização – Parte 3

No artigo anterior, mostramos como a correção direta do efeito de suavização da krigagem ordinária se processa para dados apresentando assimetria negativa, que se caracteriza por um baixo coeficiente de variação. A correção direta para esse tipo de distribuição é efetiva e pode ser usada como foi demonstrado naquele artigo.

Neste artigo, vamos tratar da questão da correção direta para distribuições simétricas. A metodologia da correção direta baseada em Yamamoto (2005) está também descrita em detalhe em Yamamoto e Landim (2013). Distribuições simétricas são especialmente convenientes para fins de análise e estimativa geoestatísticas. Observe-se que as transformações não lineares como a logarítmica e a Gaussiana procuram gerar distribuições simétricas ou aproximadamente simétricas. No caso da transformação Gaussiana, a distribuição resultante será sempre simétrica com média zero e variância unitária, não importando a forma da distribuição inicial.

Para essa demonstração, considere-se uma amostra composta por 100 pontos de dados selecionada por amostragem aleatória estratificada de uma população com 2500 pontos distribuídos em uma malha de 50 por 50 nós, como ilustra o mapa de localização da Figura 1.

A distribuição de frequências da Figura 2 mostra que a distribuição de frequências pode ser considerada normal, pois os pontos da curva acumulativa se alinham em torno de uma reta. Entretanto, o histograma não se apresenta perfeitamente simétrica, embora a amostra tenha sido extraída de uma população normal.

A análise geoestatística é feita com o objetivo de determinar o modelo de correlação espacial, por meio do variograma, que é a ferramenta que permite descrever a variabilidade espacial dos dados. Para descobrir as direções de possível anisotropia foram confeccionados os variogramas direcionais e o mapa variograma (Figura 3).

 

O mapa variograma não mostra claramente a presença de anisotropia, o que pode ser confirmada pelos variogramas direcionais. Assim, nestes casos pode-se optar pelo variograma omnidirecional, que é calculado considerando uma tolerância angular de 90º para cada lado e largura máxima muito grande (Figura 4).

O próximo passo é a krigagem ordinária, com base no modelo de correlação espacial obtido (Figura 4). A krigagem ordinária proporciona estimativas a partir da minimização da variância do erro e, por isso, elas são suavizadas. As estimativas são feitas localmente, ou seja, a partir dos pontos de dados vizinhos escolhidos por um critério, como, por exemplo, o critério dos quadrantes (Figura 5).

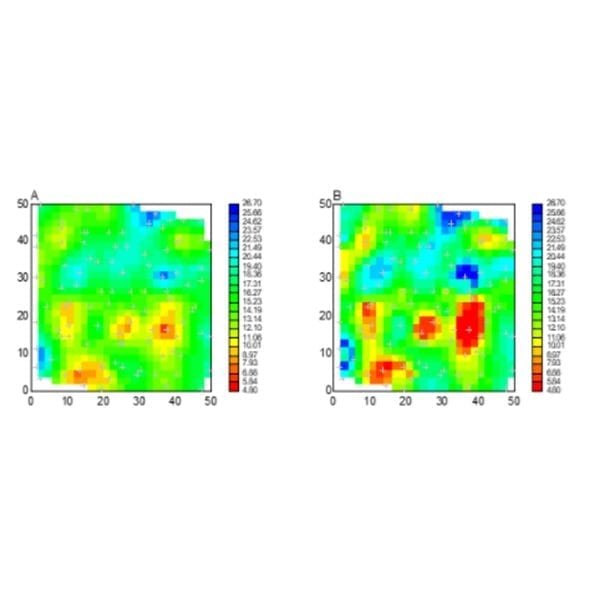
Para essa demonstração, foram selecionados dois pontos por quadrante para fins da krigagem ordinária e pós-processamento para correção do efeito de suavização (Figura 6). Como nos casos anteriores, a correção da suavização se manifesta claramente, onde os valores altos subestimados são corrigidos para cima e os valores baixos superestimados são movidos para baixo. As estatísticas descritivas das estimativas em comparação com as amostrais são apresentadas na Tabela 1.

Tabela 1: Estatísticas descritivas para os valores amostrais e krigagens.

 

Estatística	Amostra	Krigagem	Krigagem corrigida
No. Dados	100	571	571
Média	15,374	15,271	15,374
Desvio padrão	4,549	3,168	4,525
Coef. de variação	0,296	0,207	0,294
Máximo	26,852	23,639	26,702
Quartil superior	18,117	17,580	18,588
Mediana	15,618	15,206	15,692
Quartil inferior	12,476	13,219	12,349
Mínimo	4,798	6,809	4,798

 

Ao examinarmos esta tabela, verifica-se como a correção é efetiva permitindo recompor a variabilidade original, pois passa-se de um desvio padrão igual a 3,168 para 4,525, em relação ao desvio padrão amostral igual a 4.549, ou seja, a krigagem corrigida recompõe 99,5% do desvio padrão amostral. Consequentemente, a correção recupera o coeficiente de variação para um valor muito próximo ao amostral.

Agora, a comparação entre as distribuições de frequências pode ser feita graficamente (Figura 7), ou seja, verificação da reprodução do histograma (estatística de um ponto). Como se pode observar nesta figura, a krigagem corrigida proporciona uma distribuição de frequências muito próxima da amostral. Apesar da cauda inferior não estar perfeitamente reproduzida em relação à distribuição amostral, pode-se considerar a distribuição da krigagem corrigida para fins de inferência estatística. Por outro lado, a krigagem ordinária, sem correção, mostra claramente a redução da variância.

Para verificação da precisão global, resta verificar a reprodução do modelo de variograma, pois estamos interessados não apenas na distribuição espacial da variável de interesse, como também na sua variabilidade espacial. Assim, pode-se calcular os variogramas experimentais na malha regular krigada. Como neste caso, optou-se por um variograma omnidirecional, os variogramas direcionais calculados a partir da malha regular são usados para determinar um variograma médio, o que equivale em tese ao omnidirecional (Figura 8).

Nesta figura, pode-se observar que a reprodução do modelo de correlação espacial é efetiva, quando comparada com os valores da krigagem ordinária. Essa reprodução é melhor nos 2/3 da amplitude, que é a parte importante em termos de correlação espacial. Assim, para dados com distribuição simétrica de frequências, a metodologia de correção direta pode ser considerada para reprodução da distribuição e variabilidade espaciais da variável de interesse e, nesse sentido, o modelo obtido pode ser usado para fazer a inferência estatística. Assim, temos uma única imagem que apresenta tanto precisão local, como também a precisão global, em termos da reprodução do histograma e do modelo de variograma.

Nos próximos artigos, trataremos da questão da transformação não linear e sua transformada reversa não enviesada. Serão abordadas as transformações: logarítmica e a Gaussiana.

 

Referências bibliográficas

Harbaugh, J.W.; Doveton, J.H. Davis, J.C. 1977. Probability methods in oil exploration. New York, John Wiley & Sons. 269p.

Yamamoto, J.K. 2005. Correcting the smoothing effect of ordinary kriging estimates. Mathematical Geology, v. 37, n.1, p. 69-94, 2005.

Yamamoto, J.K.; Landim, P.M.B. 2013. Geoestatística: conceitos e aplicações. São Paulo, Oficina de Textos. 214p.