Como fazer a transformada Gaussiana

Dando continuidade ao artigo anterior, neste vamos abordar a transformada gaussiana que é bastante utilizada na geoestatística. Este artigo foi derivado com alterações do item 4.2: “Transformada gaussiana”, segundo Yamamoto (2020, p. 94-95).

As técnicas geoestatísticas que se baseiam nos escores normais, obtidos após a transformada gaussiana, são: a krigagem multiGaussiana e a simulação gaussiana sequencial.

A transformada Gaussiana é aquela que permite obter um histograma normal, com média zero e desvio padrão igual a um, qualquer que seja o histograma dos dados originais. Este método gera sempre um histograma simétrico e com variabilidade igual à distribuição normal.

Função de distribuição acumulada

Segundo Deutsch e Journel (1992, p. 138), a primeira condição necessária para que a função aleatória Y(x) seja normal multivariada é que sua função de distribuição acumulada seja normal:

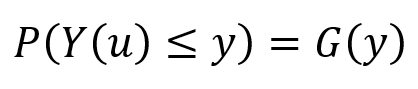
Sejam Z e Y duas variáveis aleatórias com funções de distribuições acumuladas FZ(z) e FY(y), então a transformada Y=ϕ(Z) identifica as probabilidades acumuladas correspondentes ao quantil p para Z e Y (Deutsch e Journel, 1992, p. 138):

Transformada escore normal

Se Y é uma variável normal padrão com função de distribuição acumulada FY(y)=G(y), então a transformada G-1(FZ(.)) é a transformada escore normal (Deutsch e Journel, 1992, p. 138).

Segundo Deutsch e Journel (1992, p. 138), a transformada escore normal do k-ésimo valor de z(k) é o quantil k/n da função de distribuição acumulada normal:

De acordo com esses autores, o escore normal para n/n seria igual a +∞, que necessita de tratamento desse último valor. Para evitar isso, pode-se simplesmente usar os escores uniformes, conforme:

Exemplo de aplicação

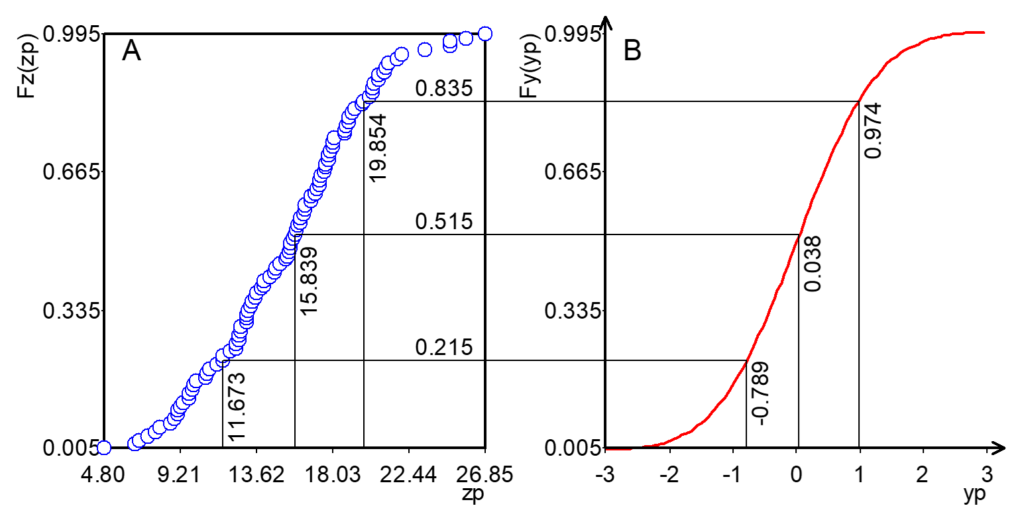
Para ilustrar a transformada Gaussiana por escores normais, considere-se o conjunto de pontos de dados simetrica100.csv, conforme a Figura 1. Três valores são usados como exemplo para determinação dos escores normais. Na Figura 1A, o valor 11,673 da variável zp é selecionado, que corresponde a uma proporção acumulada de 0,215. Este valor é então projetado na distribuição normal acumulada (Figura 1B), que resulta no escore normal igual a -0,789.

Os resultados da transformada Gaussiana se encontram representados na Figura 2.

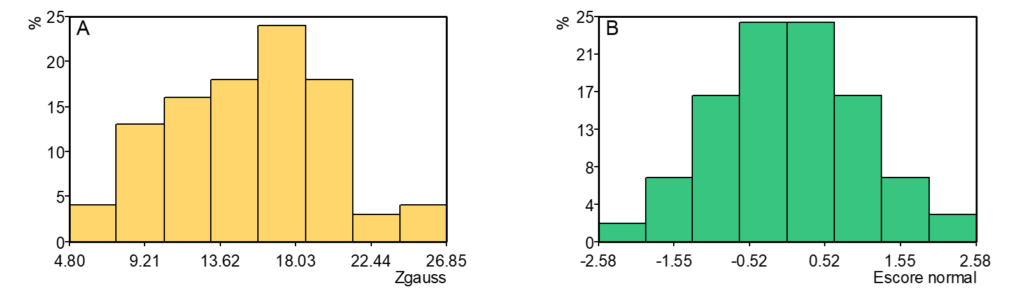
Como se pode observar nesta figura, a transformada Gaussiana garante uma distribuição de frequências perfeitamente normal, com média zero e variância próxima de um.

Considerações finais

A transformada gaussiana é extremamente conveniente para o tratamento de dados extremos, evitando assim a sua eliminação ou substituição por valores máximos estabelecidos pelo responsável pela pesquisa mineral. Salienta-se que não basta transformar os dados para escores normais, pois as técnicas da krigagem multiGaussiana e da simulação gaussiana sequencial trabalham sob a forte hipótese de multiGaussianidade dos dados. Isso significa que não apenas os dados originais devem ser normais, mas que as distribuições de dois, três ou mais pontos também sejam normais. Quem se interessar pelo teste de multiGaussianidade dos dados recomendamos consultar Yamamoto e Landim (2013, p. 88-93).

Referências bibliográficas

Deutsch, C.V.; Journel, A.G. 1992. GSLIB – Geostatistical software library and user’s guide. New York, Oxford University Press. 340p.

Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 308p.

Yamamoto, J.K.; Landim, P.M.B. 2013. Geoestatística: conceitos e aplicações. São Paulo, Oficina de Textos. 215p.

Próximo artigo

Os dois próximos artigos irão apresentar assuntos relacionados à análise geoestatística, segundo Yamamoto (2020, p. 100-141).