Isaaks e Srivastava (1989, p. 4-5) proporcionaram uma base de dados chamada walker.dat composta por 470 pontos, que foram extraídos de um conjunto completo (população) com 78000 pontos distribuídos em uma malha regular de 260 por 300 nós. Esses dados estão salvos no arquivo walker_dat.csv, que contém seis variáveis: ID, Xlocation, Ylocation, V, U e T. V e U representam teores simulados em ppm (derivados da topografia do terreno) e T uma variável indicadora. Os dados de topografia se referem ao modelo de elevação de terreno da região do Lago Walker (Nevada), conforme o esquema da Figura 1.

Fonte: https://en.wikipedia.org/wiki/Walker_Lake_(Nevada) *Segundo Isaaks e Srivastava (1989, p. 4-6)
Para termos uma ideia da distribuição espacial dos dados, podemos escrever um script em R para fazer o mapa de localização de pontos (Figura 2).

Distribuição de frequências
Uma lista desorganizada de números representando as realizações de experimentos não é facilmente assimilada (Benjamin e Cornell, 1970, p. 4). A simples tabulação dos dados brutos em uma distribuição de frequências permite obter uma primeira aproximação para verificação das características dos dados (Figura 3). A caracterização da distribuição de frequências pode ser feita tanto qualitativa como quantitativamente.

Descrição qualitativa
A descrição qualitativa da distribuição de frequências pode ser feita por sua representação na forma de histograma e curva acumulativa.
O histograma é a representação gráfica da distribuição de frequências obtida agrupando os dados em classes. O tamanho da classe é calculado como:

O número de classes pode ser determinado pela Regra de Sturges (Haan, 1977, p. 17-18):
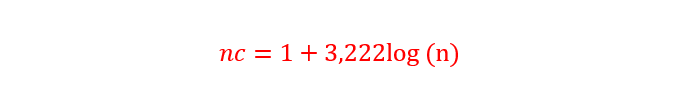
O Script GKS2.R gera o histograma (Figura 4) com o número de classes calculado pela Regra de Sturges. Para isso, torna-se necessário informar os pontos de quebra do histograma, que são definidos nas linhas 8-10. Na linha 14, o objeto h recebe o histograma desenhado. Ao se fazer a impressão do objeto h (linha 18), tem-se a listagem dos seis componentes:
- $breaks – são as quebras usadas pela função hist();
- $counts – se referem às contagens nas classes do histograma;
- $density – são os valores da função densidade de probabilidade normal;
- $mids – são os pontos médios das classes;
- $xname – é o nome da variável;
- $equidist – é uma booleana que indica se as classes são equidistantes.
Observe-se que usamos o operador $ para recuperar os componentes do objeto h. Estes componentes podem ser usados em outras aplicações que necessitem a subdivisão em classes e sua contagem.


A curva acumulativa é outra descrição qualitativa possível para a distribuição de frequências. Uma representação seria acumular as frequências nas classes do histograma, mas o resultado não seria satisfatório devido à pequena quantidade de pontos. Este tipo de curva acumulativa se chama polígonos de frequência acumulada. Para aumentar o número de pontos da curva acumulativa, pode-se aplicar a mesma estratégia de calcular o número de quebras e informar a função hist() os pontos de quebra. O Script GKS3.R permite calcular uma curva acumulativa (Figura 5) com 100 pontos, como se pode verificar na linha 5.
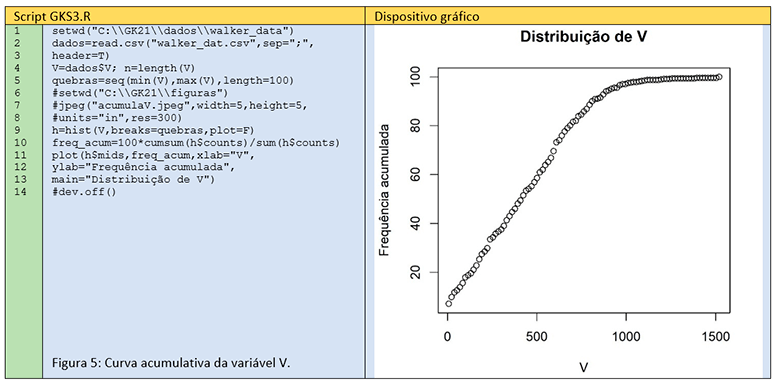
Verificar que neste script, usamos uma programação orientada a objetos na linha 5, enquanto no Script GKS2.R, fizemos uma programação com o comando for(), que teve por objetivo a finalidade didática deste artigo. Além disso, na linha 9 foi chamada a função hist() apenas para calcular as contagens nas classes, que foram usadas na linha 10 para se calcular as frequências acumuladas.
Descrição quantitativa
A descrição quantitativa de uma distribuição de frequências pode ser feita por meio das estatísticas descritivas, que por sua vez são divididas em medidas de tendência central, dispersão e forma (Figura 6).

Média ou esperança matemática:

Mediana é o valor correspondente a 50% da distribuição de frequências:

Moda é a classe mais frequente na distribuição de frequências. A determinação da moda depende das frequências de classe imediatamente anterior e posterior à classe modal. A Figura 7 mostra que a moda é deslocada para direita devido à maior frequência f3 em relação a f1.

A interpolação da moda pode ser feita com base na seguinte fórmula (Francis, 2004, p. 118):

onde L é o limite inferior da classe modal; C é a largura da classe modal; D1 é a diferença entre a maior frequência e a frequência da classe imediatamente anterior; D2 é a diferença entre a maior frequência e frequência da classe imediatamente seguinte.
Variância é uma medida de dispersão dos dados em torno da média:

Desvio padrão é simplesmente a raiz quadrada da variância:

Coeficiente de variação é uma medida adimensional da dispersão. Pode ser usada para fazer a comparação de diferentes variáveis, em termos da dispersão:
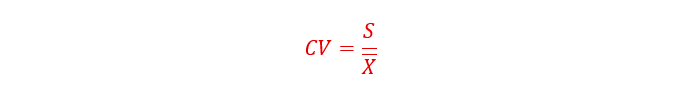
O coeficiente de assimetria é calculado como somatória de diferenças elevadas à uma potência ímpar pode resultar positivo ou negativo.

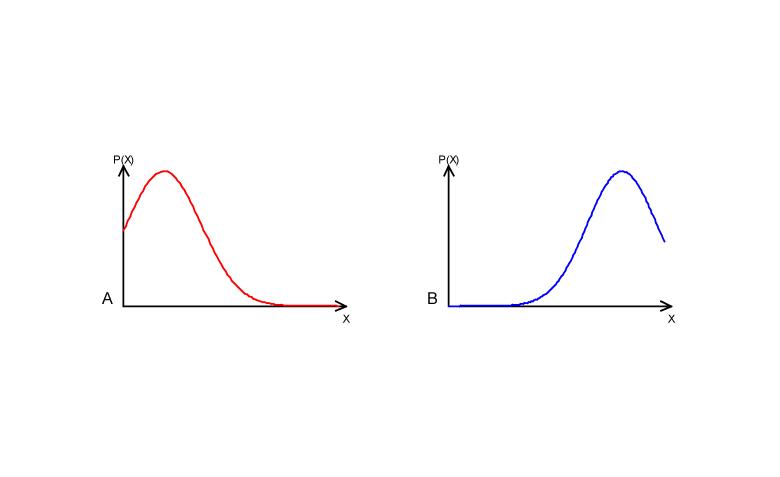
Quando o valor for positivo, tem-se assimetria positiva e quando negativo, diz-se que há assimetria negativa (Figura 8).
O coeficiente de curtose é sempre positivo, pois se trata da somatória de diferenças elevadas à uma potência par.

A curtose é usada para medir a dispersão em distribuições simétricas, como se ilustra na Figura 9.

Divisores da distribuição de frequências
Como vimos anteriormente, a mediana é o valor correspondente a 50% da distribuição de frequência. Trata-se de um divisor da distribuição de frequências em 50%. Existem outros divisores que podem ser usados, conforme a Figura 10.

A amplitude interquartil, que é uma medida de dispersão, pode ser calculada como a diferença entre o 3º e 1º:

Script GKS4.R
Nesse script, tem-se a função descritivas() que permite calcular todas as estatísticas descritivas apresentadas neste artigo. Esta função chama a biblioteca “moments” que precisa ser instalada. Este pacote permite calcular os coeficientes de assimetria e curtose. Há também a chamada da função definida pelo usuário chamada moda_francis(), que é chamada para calcular a moda de uma distribuição de frequências. No caso dessa função, se a classe modal for a primeira ou a última, a moda é dada pelo ponto médio da classe modal. Para evitar isso, pode-se aumentar o número de classes, de tal modo que a classe modal não seja a primeira ou a última. Devido à extensão desse script não listaremos no texto do artigo, mas está disponível no site.


Observações importantes:
Para executar os scripts, observe os diretórios nos quais estão gravados os arquivos. A título de sugestão, o Leitor poderá criar um diretório na raiz do disco C, como C:\GK21. Debaixo de GK21, pode criar os subdiretórios dados e figuras: C:\GK21\dados e C:\GK21\figuras, respectivamente. Todos os scripts a serem publicados doravante seguirão os diretórios apresentados.
Dados e scripts
Para acompanhar este artigo, deve-se ter acesso aos scripts GKS1, GKS2, GKS3 e GKS4, clicando aqui, bem como ao conjunto de dados walker_dat.csv. Este arquivo pode ficar no diretório seguinte:
C:\GK21\dados\walker_data
Referências bibliográficas
Benjamin, J.R.; Cornell, C.A. 1970. Probability, statistics and decision for civil engineers. Mineola, Dover Publications Inc. 684p.
Francis, A. 2004. Business mathematics and statistics. Hampshire, South-Western. 665p.
Haan, C.T. 1977. Statistical methods in hydrology. Ames, The Iowa State University Press. 378p.
Isaaks, E.H.; Srivastava, R.M. 1989. An introduction to applied geostatistics. New Yrok, Oxford University Press. 561p.
Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 308p.




