Análise De Variância (Anova) E Regressão Linear Múltipla – Parte 6

Script Em R Para Regressão Linear Múltipla

Neste artigo, iremos tratar da resolução do sistema de equações de regressão linear múltipla (1) usando a codificação alternativa. O novo script que se apresenta neste artigo é praticamente o mesmo do anterior (Script GK12), mas o objetivo é fazer a interpretação dos coeficientes da regressão múltipla, em termos dos valores médios dos níveis do fator.

Os dados de lixiviação bacteriana (Lapin, 1998, p. 546), obtidos com três variedades de bactérias, codificados alternativamente se encontram na Tabela 1.

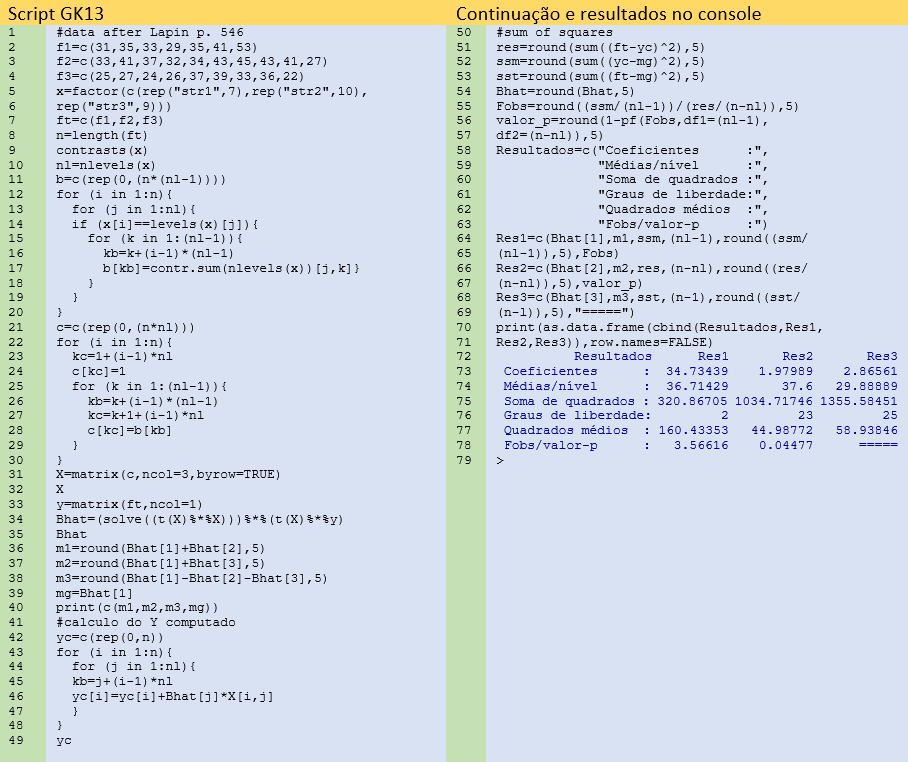
O Script GK13 permite calcular os coeficientes da regressão linear múltipla, calcular a variável dependente nos pontos de observação e fazer a conversão em soma de quadrados, para fins da análise de variância.

Como se pode notar, o Script GK13 é exatamente o mesmo que o anterior (Script GK12), mas com a linha 17 alterada para a codificação alternativa. Além disso, como os coeficientes são diferentes (Tabela 2), as médias por nível são calculadas nas linhas 36-38, como uma combinação linear dos coeficientes.

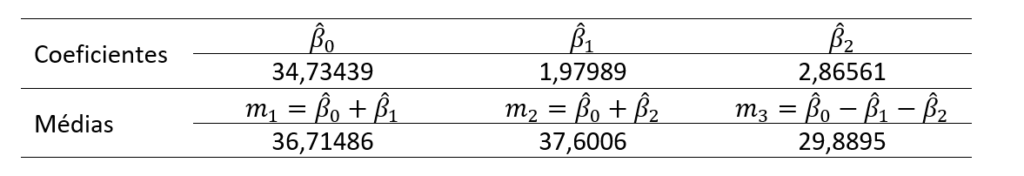
Na Tabela 2, verifica-se que o intercepto é igual à média geral ou grande média. As médias por nível resultam de operações aritméticas entre os coeficientes (linhas 36-38). A equação de regressão múltipla pode ser escrita como:

A equação de regressão aplicada nos níveis definidos pela codificação alternativa resulta nas médias dos níveis (Tabela 3)

Os demais resultados são exatamente iguais àqueles obtidos por codificação indicadora (Script GK12), bem como com aqueles calculados manualmente (considerando diferenças por arredondamento).

Referência bibliográfica

Lapin, L.L. 1998. Probability and statistics for modern engineering. Prospect Heights, Waveland Press. Inc. 810p.

Próximos artigos

Nos próximos artigos, iremos apresentar alternadamente conceitos de álgebra linear e testes de hipóteses, sempre acompanhados da teoria, demonstração de cálculos feitos manualmente e scripts em R.