Análise De Variância (Anova) E Regressão Linear Múltipla – Parte 5

Script Em R Para Regressão Linear Múltipla

No artigo anterior, apresentamos a teoria da regressão linear múltipla com variáveis independentes categóricas. Essas variáveis não podem ser processadas diretamente, mas somente por meio de suas funções indicadoras.

O sistema de equações da regressão linear múltipla pode ser escrito, em termos matriciais, como (Rencher, 2002, p. 324):

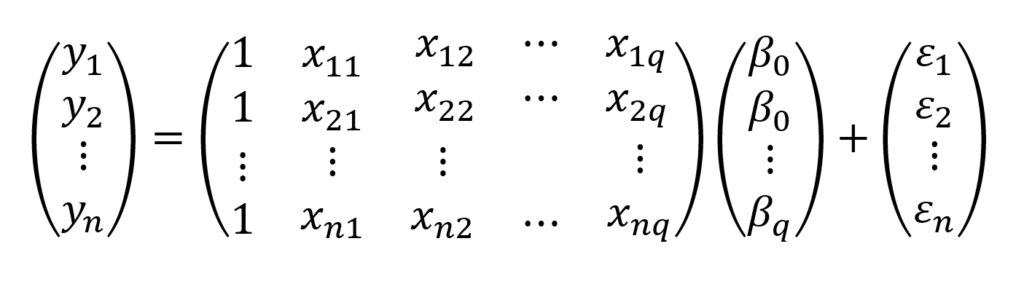
Na Tabela 1, tem-se os elementos para o sistema de equações (1), para determinação dos coeficientes.

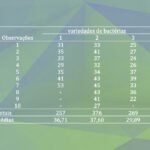
Tabela 1: Matriz X do sistema de equações (2) para regressão linear múltipla, com a codificação por variáveis indicadoras conforme variedades de bactérias (Lapin, 1998, p. 546).

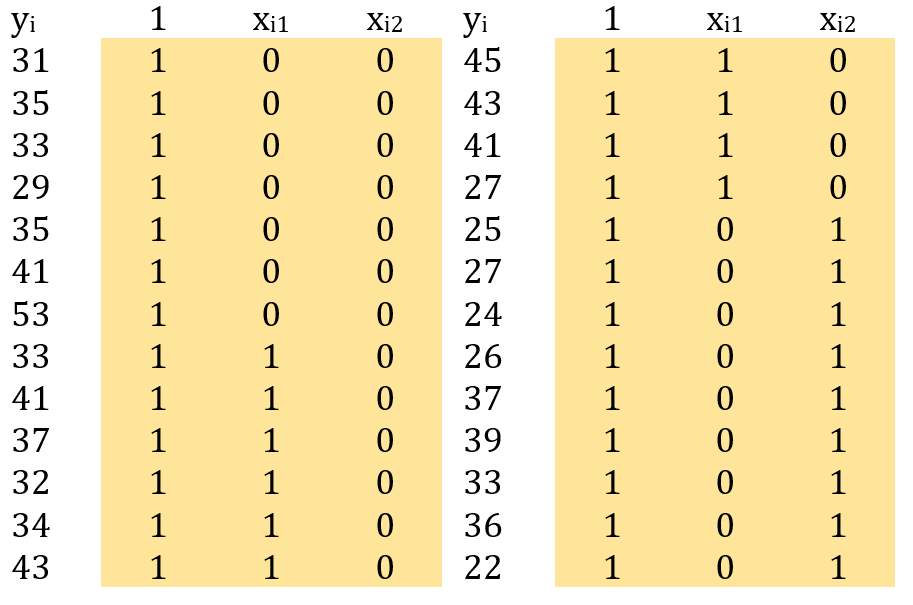
Primeiro, seja a matriz X e o vetor y definidos na Tabela 1. O objetivo é encontrar os coeficientes da regressão linear múltipla (equação 1). No Script GK12, após a entrada dos dados, define-se a matriz de contrastes como o objeto b; em seguida, cria-se o objeto c que é praticamente a matriz X (linha 30).

O vetor y é definido na linha 32. Os coeficientes resultam do comando da linha 33, ou seja, em uma única linha se obtém a solução da regressão linear múltipla. Trata-se de uma grande vantagem da linguagem R que é orientada a objetos.

Os coeficientes da regressão múltipla dependem do tipo de codificação: indicadora ou alternativa. Para a codificação indicadora, o Script GK12 produz os seguintes resultados (Tabela 2). Verifica-se que o intercepto é a própria média do primeiro nível e as demais médias são derivadas por meio de operações aritméticas entre os coeficientes (Tabela 2).

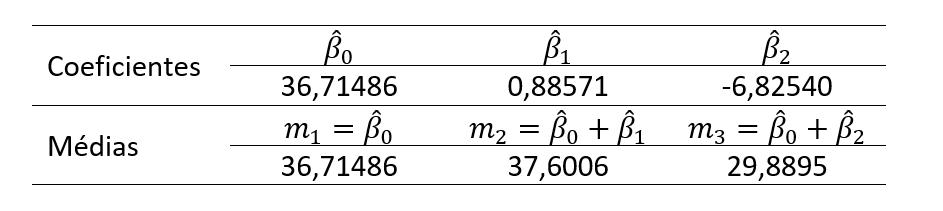
Assim, a equação pode ser expressão como:

Aplicando-se a equação obtida para os níveis (Tabela 1), tem-se as suas médias (Tabela 3). Em seguida, calcula-se as somas dos quadrados, conforme as linhas 49 a 51 do Script GK12. Depois, são determinados o valor de F observado e o valor-p (resultados no Script GK12). Demonstra-se, dessa forma, a conexão entre a análise de variância e a regressão linear múltipla.

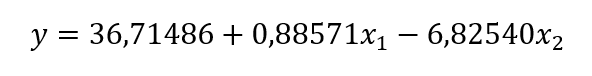
Este artigo apresentou um script para regressão linear múltipla e análise de variância com um fator para dados de lixiviação bacteriana em minérios de cobre de baixo teor. O Script GK12 pode ser facilmente adaptado para os dados do Leitor.

Referências bibliográficas

Lapin, L.L. 1998. Probability and statistics for modern engineering. Prospect Heights, Waveland Press. Inc. 810p.

Rencher, A.C. 2002. Methods of multivariate analysis. New York, John Wiley & Sons. 708p.

Próximo artigo

Em continuidade, o próximo artigo irá tratar da resolução do sistema de equações (1), mas com a matriz dos coeficientes obtida por codificação alternativa, por meio de um script em R.

Os coeficientes são diferentes dos obtidos para a codificação indicadora e, dessa forma, são interpretados em termos das médias dos níveis.