Análise de variância (anova) e regressão linear múltipla – parte 4

Dando sequencia ao artigo anterior, a regressão linear múltipla envolve várias variáveis independentes, que podem ser contínuas ou discretas. Neste artigo, vamos tratar do caso em que as variáveis independentes são todas categóricas ou fatores, sendo que cada fator apresenta alguns níveis. Conforme a definição de variável categórica, ela pode ser composta por tipos.

Por exemplo, em uma bacia sedimentar ocorrem várias litologias, que são os tipos da variável categórica denominada litologia. Os tipos dessa variável, por exemplo, podem ser: arenito, siltito, argilito, marga, calcário e folhelho.

Assim, a variável litologia é composta por seis tipos. Variáveis categóricas não podem ser manipuladas diretamente, mas somente por meio de suas funções indicadoras. Em seguida, apresenta-se a fundamentação teórica sobre a regressão linear múltipla. Como mencionado anteriormente, é importante o entendimento da teoria para aplicar corretamente uma função de biblioteca da linguagem R, no caso a função lm(), que permite fazer a regressão linear simples ou múltipla.

Na regressão linear múltipla, expressa-se a variável dependente Y em uma amostra com n observações como uma função linear das variáveis independentes X mais um erro aleatório ε (Rencher, 2002, p. 323):

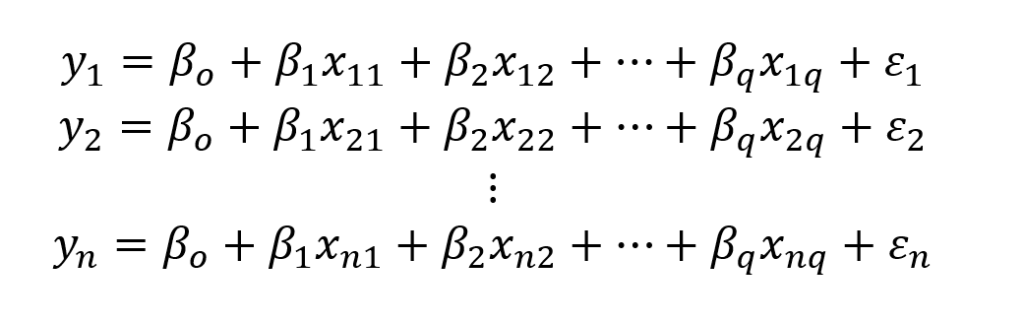
Em termos matriciais, Rencher (2002, p. 324), o sistema (1) pode ser escrito como:

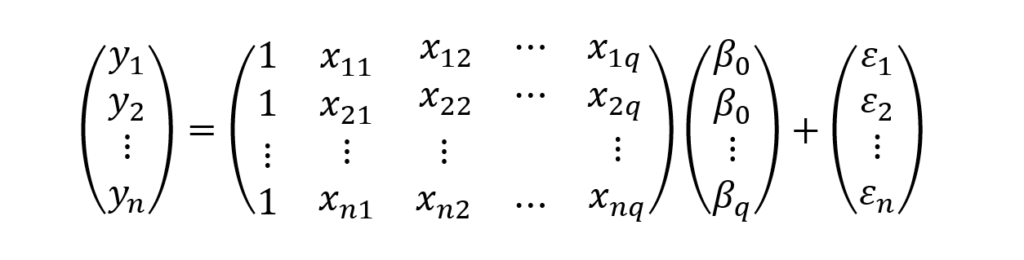
ou

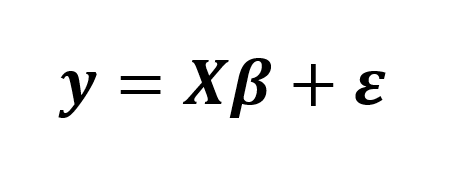
Segundo Rencher (2002, p. 324), para fins de estimação e teste de hipóteses, n deve ser maior que (q+1). Assim, as estimativas dos mínimos quadrados para β podem ser obtidas como (Rencher, 2002, p. 325):

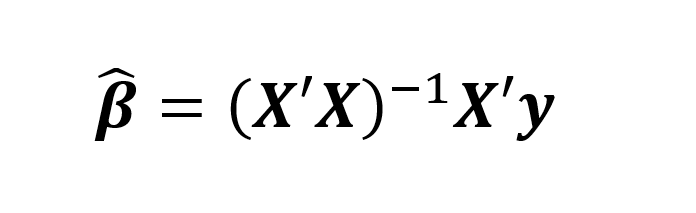
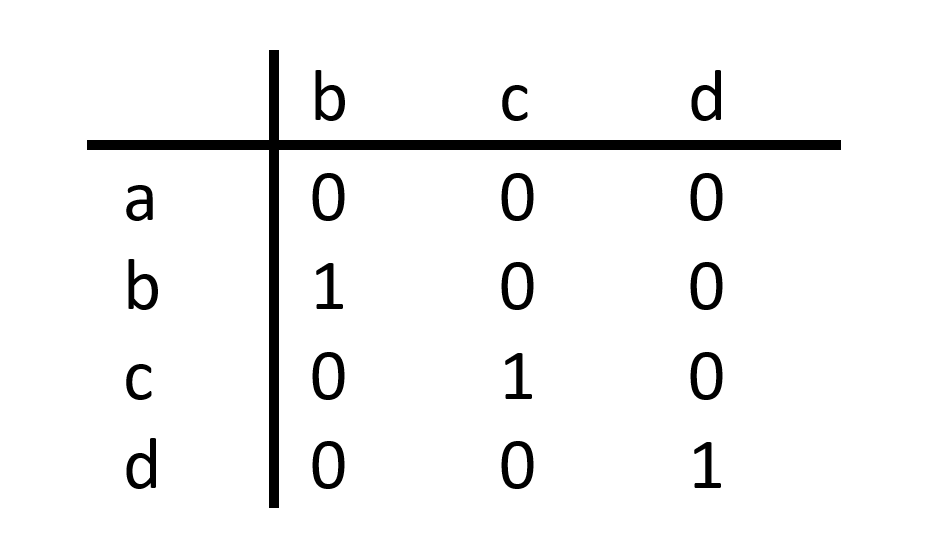
O vetor y constitui as observações combinadas de todos os níveis do fator, mas a matriz X precisa ser codificada como funções indicadoras, como se expõe a seguir. Empregando a mesma notação usada anteriormente, tem-se n_t níveis e, portanto, n_t-1 variáveis tipo dummy ou variáveis indicadoras. Nas equações (1) e (2), os elementos da matriz X:  são as variáveis indicadoras, onde q é igual ao número de níveis menos um. Para exemplificar a codificação por variáveis indicadoras, seja um fator com quatro níveis: a, b, c e d, que gera uma matriz de contrastes (Tabela 1).

Tabela 1: Matriz de contrastes para uma variável categórica com quatro níveis.

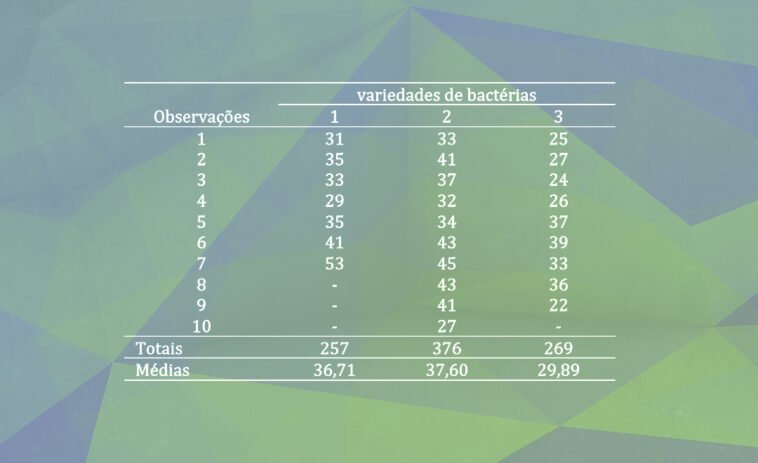
Apesar de ser repetitivo, vamos colocar novamente a tabela dos dados de lixiviação bacteriana para recuperação de cobre (Tabela 2), pois facilita o Leitor.

Como são três variedades de bactérias (Tabela 2), tem-se duas variáveis indicadoras que podem ser obtidas da matriz de contrastes (Tabela 1), restringindo-a até a letra c. Em R, tem-se a função contrasts() que faz a codificação indicadora (Script GK10).

Pode-se fazer também uma codificação alternativa, com base na função contr.sum(), conforme o Script 5.54.

Tabela 3: Matriz X do sistema de equações (2) para regressão linear múltipla, com a codificação por variáveis indicadoras conforme variedades de bactérias.

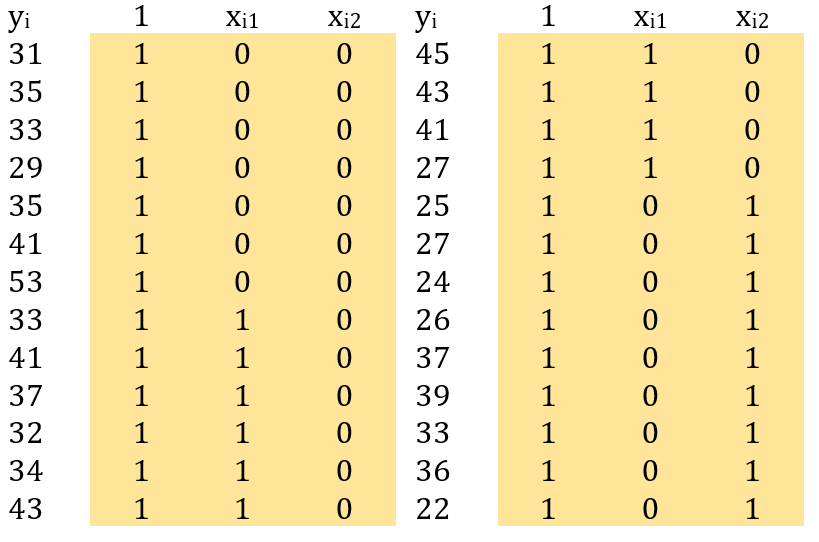
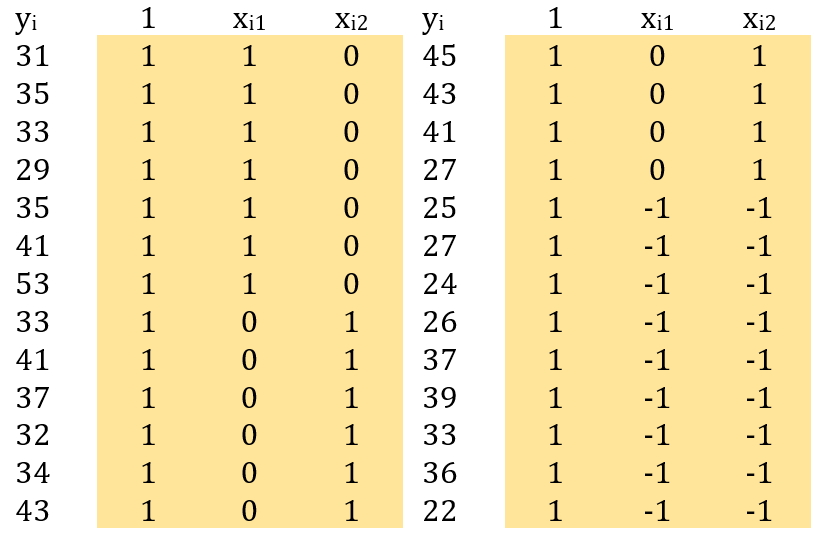
Como se pode verificar na Tabela 3, há uma coluna de valor unitário que se refere ao intercepto, ou seja, βo nas equações (1) e (2). Pode-se empregar a codificação alternativa conforme a matriz de contrastes obtida no Script GK11. A Tabela 4 apresenta a matriz dos coeficientes X, com base na codificação alternativa.

Referências bibliográficas

Lapin, L.L. 1998. Probability and statistics for modern engineering. Prospect Heights, Waveland Press. Inc. 810p.

Rencher, A.C. 2002. Methods of multivariate analysis. New York, John Wiley & Sons. 708p.

Próximo artigo

Em continuidade, o próximo artigo irá tratar da resolução do sistema de equações (2), por meio de um script em R.