Análise de Variância (Anova) E Regressão Linear Múltipla – Parte 3

Scripts Em R Para Anova – Um Fator

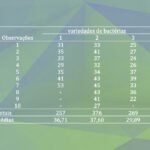
Neste artigo, apresentaremos um script para fazer a análise de variância de um critério, seguindo a metodologia descrita no artigo anterior. Os resultados da execução desse script estão de acordo com os cálculos efetuados manualmente. Os dados de lixiviação bacteriana (Tabela 1 – artigo anterior) são introduzidos como objetos f1, f2 e f3 (linhas 2-4). A variável nt indica o número de níveis do fator. Os valores n1, n2 e n3 representam os tamanhos dos objetos f1, f2 e f3, respectivamente. As médias m1, m2 e m3 são calculadas por meio da função mean() do R. A variável mg recebe a grande média ou média geral (linha 9). Feito isso, calcula-se as somas dos quadrados (linhas 11 e 12). Observe-se que no R, pode-se fazer uma somatória de diferenças ao quadrado usando um único comando. Por exemplo, se não houvesse essa possibilidade o comando equivalente seria efetuar a somatória para calcular sqf1:

A natureza orientada a objetos da linguagem R torna mais simples a programação, além de deixar o código mais claro.

Em seguida, passa-se ao cálculo dos quadrados médios que são obtidos pela divisão da soma de quadrados pelos graus de liberdade (linhas 25-27). A razão F é determinada na linha 18, cujo valor é usado para calcular o valor-p, por meio da função pf() da biblioteca do R.

Usando os recursos da linguagem R, pode-se fazer uma regressão, cujos resultados podem ser sumariados na forma de uma análise de variância, como se encontra no Script GK9. O script anterior nos auxilia a entender o procedimento da análise de variância com um fator. O entendimento do processo é importante para analisar e interpretar os resultados. Evidentemente, após o conhecimento da metodologia, pode-se usar diretamente a função de biblioteca do R.

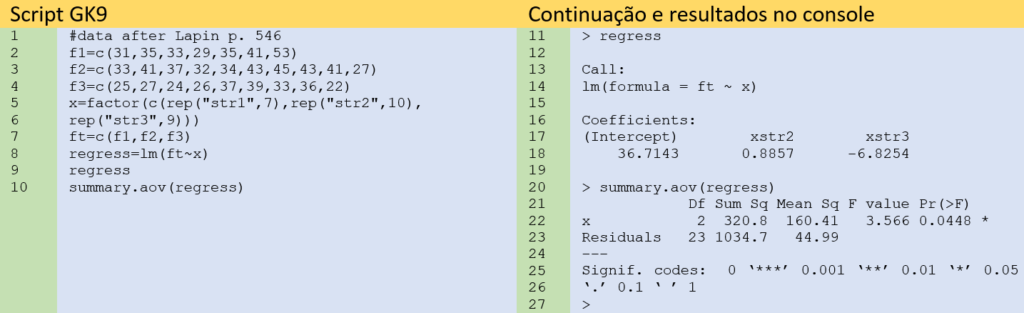
No Script GK9, a análise de variância foi feita a partir dos resultados da regressão obtida por meio da função lm() do R. Nos resultados do Script GK9, verifica-se o valor do intercepto igual a 36,7143 que é exatamente igual à média m1. Os demais coeficientes combinados dão origem às demais médias, como será abordado nos próximos artigos.

Próximo artigo

Como foi mencionado, a regressão linear múltipla pode ser usada para fazer a análise de variância de um fator. Tendo em vista que a variável independente é um fator (categórica) com vários níveis, procede-se à codificação indicadora, como será descrito no próximo artigo.