Análise de Variância (Anova) E Regressão Linear Múltipla – Parte 2

Neste tipo de análise de variância, isola-se os efeitos de uma única variável categórica (tratamentos) sobre os resultados das amostras (Burt et al. 2009, p. 434). O procedimento da análise de variância ajuda a traduzir os dados amostrais em uma ação ou providência (Lapin, 1998, p. 551).

Para acompanhar o desenvolvimento da análise de variância de um critério, sejam o dados de lixiviação bacteriana em minério de cobre de baixo teor (Tabela 1), onde o engenheiro de minas precisa avaliar as variedades de bactérias na recuperação de cobre (Lapin, 1998, p. 546).

O engenheiro de minas deve determinar se uma variedade de bactéria difere na eficiência de recuperação de cobre por lixiviação, então se pode começar testando se a média populacional é a mesma para cada variedade, segundo Lapin (1989, p. 547):

Assim, testa-se H_o contra a hipótese alternativa que pelo menos uma média é diferente.

Tabela 1: Dados de recuperação de cobre (lb/ton) por lixiviação bacteriana em minério de baixo teor (Lapin, 1998, p. 546).

O modelo de análise de variância (ANOVA) pode ser formulado como uma equação linear (Lapin, 1989, p. 549; Burt et al. 2009, p. 435):

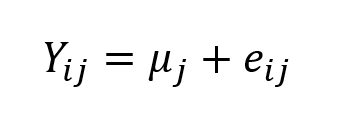
Onde: µ_j é a média populacional do j-ésimo tratamento (colunas da Tabela 5.37); e_ij é erro aleatório associado ao j-ésimo tratamento e à i-ésima observação.

O tamanho combinado da amostra é (Lapin, 1989, p. 549):

A média de cada tratamento (nível ou fator) pode ser calculada como (Lapin, 1989, p. 550):

Dessa forma, a média geral ou grande média fica:

A análise de variância começa pela decomposição da variação total em suas componentes explicada e não explicada, como se descreve a seguir. Segundo Burt et al. (2009, p. 440), o desvio da observação Yij da média geral pode ser dividido em duas partes:

Elevando ao quadrado ambos os lados da equação (3), de acordo com Burt et al. (2009, p. 442):

Pode-se denominar os componentes como:

Onde SQTO é a soma total dos quadrados, SQEX é a soma dos quadrados explicada e SQNE é a soma dos quadrados não explicada.

Seguindo o exemplo numérico, pode-se fazer os cálculos:

A soma dos quadrados não explicada pode ser determinada conforme a Tabela 2 (Lapin, 1989, p. 554).

Tabela 2: Cálculo da soma dos quadrados não explicada para dados de recuperação de cobre (Lapin, 1989, p. 554).

A soma total dos quadrados é simplesmente a somatória das diferenças ao quadrado entre as observações Y_ij em relação à média global (34,734), que dá:

Pode-se organizar as variâncias em uma tabela de análise de variância (Lapin, 1989, p. 555), como está na Tabela 3.

Tabela 3: Análise de variância e teste F para recuperação de cobre por lixiviação bacteriana (Lapin, 1989, p. 555).

Para se calcular o valor-p, pode-se usar a função pf() da biblioteca do R:

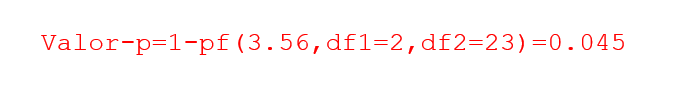
Como o valor-p é menor que 0,05, rejeita-se a hipótese nula Ho e, portanto, aceita-se a hipótese alternativa que pelo menos uma média é diferente.

 Os cálculos quando efetuados manualmente ajudam a entender as fórmulas envolvidas na análise de variância de um fator. Além disso, esse procedimento auxilia a elaboração de scritps.

Referências bibliográficas

Burt, J.E.; Barber, G.M.; Rigby, D.L. 2009. Elementary statistics for geographers. New York, The Guilford Press. 653p.

Lapin, L.L. 1998. Probability and statistics for modern engineering. Prospect Heights, Waveland Press. Inc. 810p.

Próximo artigo

No próximo artigo, iremos desenvolver um script em R que faz a análise de variância de um fator, conforme a metodologia descrita. Além disso, outro script irá mostrar como se pode fazer esse mesmo trabalho usando funções de biblioteca do R – lm() e summary.aov().