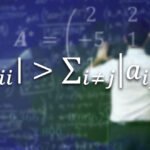Quando se trabalha com a análise de superfícies de tendência, deve-se testar se a superfície ajustada é estatisticamente significante ou não. Esse teste é geralmente feito por meio da análise de variância e teste F.
Com o aumento do grau do polinômio bivariado, gera-se mais coeficientes que acabam se ajustando melhor aos dados, mas com um custo que a superfície de alto grau tenderá a apresentar artefatos e, consequentemente, estatisticamente não significativa.
Yamamoto (2020, p. 149-157) aborda a questão da análise de variância e teste F para verificação do ajuste de superfícies de tendência polinomiais. A variação total é dividida em duas componentes: explicada pela regressão e não explicada devido aos resíduos. O Quadro 1 resume o procedimento de análise de variância e teste F, onde se determina o valor de F observado (F observado).

A partir do valor de F observado, pode-se calcular a área sob a distribuição F com (nc-1) graus de liberdade no numerador e com (n-nc) graus de liberdade no denominador. A Figura 1 representa uma distribuição F com indicação da área α, que corresponde ao valor de F crítico.

Utilizava-se, geralmente, uma tabela da distribuição F com os graus de liberdade do numerador e denominador para se determinar o valor de F crítico. Mas, atualmente, calcula-se diretamente o valor-p (α) conforme o valor de F observado, usando a função pf() da linguagem R.

Para o teste F, formula-se as seguintes hipóteses (Davis, 2002, p. 408):

Segundo a hipótese nula, testa-se se os coeficientes da superfície de tendência são iguais a zero (sem tendência alguma), segundo Davis (2002, p. 408). O teste F se dava pela comparação do F observado em relação ao F crítico.
Se o valor de F observado fosse maior que o F crítico, diz-se que a superfície é estatisticamente significativa. Na verdade, quando isso acontece significa que a área sob a distribuição F é menor que α e, portanto, na zona de rejeição de Ho. Atualmente, calcula-se o valor-p, se este for menor que 0,05 (nível de significância), rejeita-se a hipótese nula e se aceita a hipótese alternativa H1.
Nesta série de artigos, vamos abordar a análise de variância (ANOVA) para fazer a comparação simultânea entre médias de diversas amostras ou para verificar a variabilidade conforme as fontes de variação, baseada no fato que a variância de uma soma de variáveis aleatórias independentes (não correlacionáveis entre si) é igual à soma das variâncias dessas variáveis (Landim, 2003, p. 75). Usando a mesma terminologia desse autor, a análise de variância pode ser expressa como:

A variância total é a dispersão verificada em relação à média geral, enquanto a variância dentre amostras é aquela obtida em cada amostra e a variância entre amostras é a variação da média de cada amostra em relação à média geral (Landim, 2003, p. 75).
Os procedimentos para análise de variância foram desenvolvidos para auxiliar pesquisadores interessados em experimentos agrícolas (Burt et al. 2009, p. 432). Segundo esses autores, o objetivo da análise de variância é a avaliação de diferentes sementes, fertilizantes, métodos de lavoura e níveis de irrigação para determinar os níveis e combinação dos fatores que levam à maior produtividade.
Segundo Crawley (2015, p. 150), a técnica da análise de variância é usada quando todas as variáveis explanatórias são categóricas, que são chamados fatores, sendo que cada fator pode ter dois ou mais níveis. Quando há um único fator com três ou mais níveis, o procedimento se denomina análise de variância de um fator e quando há dois ou três fatores se usa a análise de variância de dois ou três fatores, respectivamente (Crawley, 2015, p. 150).
Além da análise de variância propriamente dita, esta série irá tratar também da regressão linear múltipla, onde as variáveis independentes são categóricas, ou seja, fatores que são codificados como funções indicadoras usando a matriz de contrastes. Assim, começaremos com a análise de variância com um fator e, em seguida, passaremos à análise de variância com dois fatores, que implica em maior complexidade devido às interações entre os fatores.
Referências bibliográficas
Burt, J.E.; Barber, G.M.; Rigby, D.L. 2009. Elementary statistics for geographers. New York, The Guilford Press. 653p.
Crawley, M.J. 2015. Statistics – An introduction using R. West Sussex, John Wiley & Sons. 339p.
Davis, J.C. 2002. Statistics and data analysis in geology. New York, John Wiley. 3rd edition. 638p.
Landim, P.M.B. 2003. Análise estatística de dados geológicos. São Paulo, Editora UNESP. 253p.
Yamamoto, J.K. 2020, Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 308p.
Próximos artigos
Os próximos artigos tratarão da análise de variância de um fator e regressão linear múltipla, cujos coeficientes podem ser interpretados em termos das médias dos níveis do fator.