Matriz Estritamente Diagonal Dominante
Nos artigos anteriores, o método iterativo de Gauss Seidel foi exemplificado com um sistema de equações que apresentava convergência para a solução dentro de uma tolerância especificada. Entretanto, nem sempre isso é possível, pois depende da matriz dos coeficientes A ser estritamente diagonal dominante. Define-se uma matriz estritamente diagonal dominante por linhas, se (Quarteroni et al. 2007, p. 262):
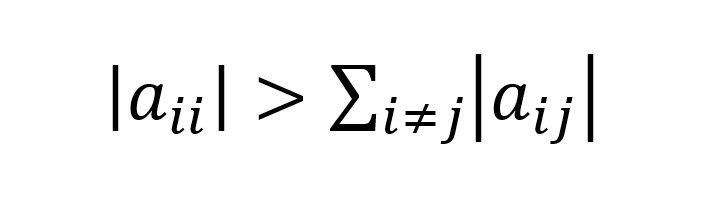
Como se pode verificar, o elemento da diagonal principal em módulo deve ser maior que a soma dos demais elementos da linha.
Por exemplo, seja a matriz dos coeficientes (Quarteroni et al. 2007, p. 132):
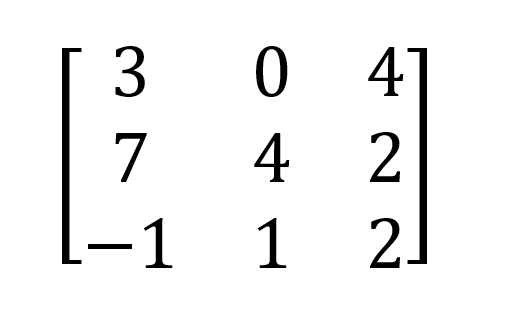
Pode-se observar que esta matriz não é estritamente diagonal dominante, pois os elementos da diagonal são menores que a soma dos demais elementos da linha. Um algoritmo bem simples para verificação desta condição se encontra no Script GK6.R, que recebe uma matriz e retorna FALSO ou VERDADEIRO.

Este script foi baseado em código previamente publicado e disponível na Web. Esta é uma das vantagens da linguagem R, qual seja, a grande disponibilidade de códigos prontos e confiáveis.
Um exemplo de um sistema de equações lineares, cuja matriz dos coeficientes não é estritamente diagonal dominante, é aquele proposto por Dunn e Parberry (2011, p. 131):

O Script GK4.R foi alterado para processar o sistema de equações (3), conforme apresentado no Script GK7.R.

Como se observa, o resultado obtido, mesmo com 500 iterações, não converge para a solução exata x’=[3,7,-2], obtida por meio da função de biblioteca solve().
Referências bibliográficas
Dunn, F.; Parberry, I. 2011. 3D Math primer for graphics and game development. Boca Raton, CRC Press. 824p.
Quarteroni, A.; Sacco, R.; Saleri, F. 2007. Iterative methods for solving linear systems. In: Numerical Mathematics. Texts in Applied Mathematics, V. 37, p. 123-181. New York, Springer.
Próximos artigos
Nos próximos artigos, pretende-se intercalar tópicos ligados à álgebra linear com aqueles referentes à estatística inferencial, sobretudo aos métodos usados para teste de hipóteses. Todos esses artigos serão derivados de novo livro em preparação: R na prática.





