Resenha Geoestatística : ” Geoestatística Mineira “
Na série Retrospectiva da Geoestatística de hoje, a resenha do livro “Geoestatística Mineira”, de Journel e Huijbregts é o foco.
Journel e Huijbregts (1978) publicam o livro intitulado “ Geoestatística Mineira ” (“Mining Geostatistics”), que permanece até hoje como uma obra de referência.
Na mesma linha de Michel David, este livro apresenta a teoria acompanhada de ilustrações e programas de computador em Fortran. Este livro está dividido em oito capítulos:
I Geoestatística e aplicações mineiras;
II Teoria das variáveis regionalizadas;
III Análise estrutural;
VI Estudos de casos de análise estrutural;
V Krigagem e a estimativa in situ de recursos;
VI Seleção e estimativa de reservas recuperáveis;
VII Simulação de depósitos;
VIII Introdução à geoestatística não linear.
Definição de termos e o variograma como ferramenta estrutural
O capítulo I contempla uma introdução e uma revisão dos métodos aplicados na indústria mineral. A Teoria das variáveis regionalizadas é abordada no capítulo II, onde o autor conceitua claramente os termos comumente empregados em geoestatística, tais como: variável regionalizada, função aleatória, inferência estatística, variância de estimativa, variância de dispersão, regularização, cálculo da função variograma médio e limites de discretização do bloco, rotina para cálculo da função variograma, funções auxiliares e as cartas com as variâncias de estimativas pré-calculadas. A Figura 1 ilustra o variograma como ferramenta estrutural (Journel e Huijbregts, 1978, p. 38).
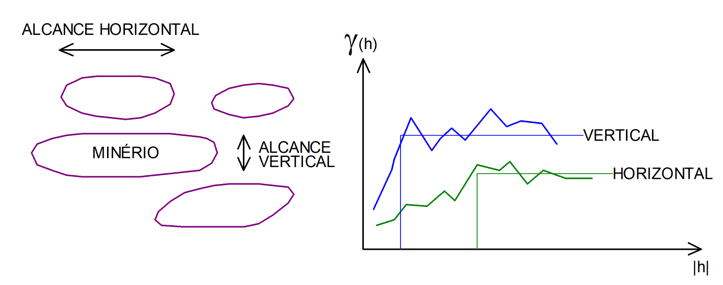
A variância de estimativa
Segundo Journel e Huijbregts (1978, p. 55), o variograma 2ϒ(h) pode ser interpretado como uma variância de estimativa elementar de uma variável Z(x) por uma outra variável Z(x+h) a uma distância h de Z(x):
![]()
Definição
A variância de estimativa é formalmente definida como a variância do erro, conforme (Journel e Huijbregts, 1978, p. 48):
![]()
Onde: ![]()
é o erro dada pela diferença entre o teor do bloco V e o teor da sondagem intersectando o centro desse bloco;
Quando o bloco é calculado a partir de n pontos de dados vizinhos![]()
e o estimador sendo uma função dos dados disponíveis
![]()
a variância de estimativa pode ser calculada como (Journel e Huijbregts, 1978, p. 51):
![]()
Variância de estimativa e de dispersão
A partir da equação (3) se desenvolve a variância de estimativa, considerando o estimador da krigagem ordinária, como se apresenta neste livro. Outro conceito relacionado à incerteza se refere à variância de dispersão, que se desenvolve a partir da seguinte relação, segundo Journel e Huijbregts (1978, p. 63):
![]()
Onde ZV(x) corresponde ao teor médio das unidades individuais
![]()
Considerando a hipótese de estacionaridade da variável aleatória Z(x), a esperança estacionária é por definição a variância de dispersão das unidades individuais v dentro de V (Journel e Huijbregts, 1978, p. 63):
![]()
Assim, pode-se apresentar a relação de aditividade de variâncias de dispersão de Krige, conforme segue (Journel e Huijbregts, 1978, p. 67):
![]()
Segundo esses autores, a expressão (3) significa que a dispersão da unidade v dentro do depósito G é igual à soma da dispersão de v no bloco V e a dispersão desses blocos V dentro do depósito G.
O cálculo do valor médio de ϒ(h) é de grande importância em geoestatística, pois as principais operações (variâncias de estimativa e de dispersão e krigagem) dependem disso (Journel e Huijbregts, 1978, p. 95):
![]()
Onde
![]()
é o valor médio da função ϒ(h) quando uma extremidade do vetor h descreve o domínio v e outra extremidade descreve independentemente o domínio v’. Esse valor pode ser calculado numericamente, onde a integral é substituída por uma somatória (Journel e Huijbregts, 1978, p. 97):
![]()
A equação (5) implica que o domínio é discretizado, conforme os valores máximos sugeridos por Journel e Huijbregts (1978, p. 97):

Journel e Huijbregts (1978, p. 103-108) proporcionam as rotinas GBAR e a função F, que permitem calcular o e as funções auxiliares, respectivamente.
Capítulo 3 – Análise Estrutural
O Capítulo III é intitulado análise estrutural, que consiste na construção de um modelo de variograma que caracteriza, de uma forma operacional, as principais feições da regionalização (Journel e Huijbregts, 1978, p. 148).
O efeito pepita surge do fato que quando se estuda teores de ouro em testemunhos de sondagem, duas amostras próximas têm teores Z(x) e Z(x+h) que diferem consideravelmente quando uma tem uma pepita e a outra não (Journel e Huijbregts, 1978, p. 151). Segundo esses autores, esse termo é empregado para caracterizar a influência residual de todas as variabilidades com amplitudes (ao) muito menores que as distâncias de observação disponíveis (h >> ao).
Os demais itens deste capítulo tratam da questão da análise estrutural propriamente dita. A função GAM, para cálculo da função variograma, é disponibilizada (Journel e Huijbregts, 1978, p. 185). Como regra prática para o cálculo de variogramas experimentais, deve-se considerar no mínimo 30-50 pares de pontos, situados a uma distância |h| < L/2, onde L é a dimensão do campo (Journel e Huijbregts, 1978, p. 194).
Estudos de casos de análise estrutural são apresentados no Capítulo IV, entre os quais o mesmo usado por David (1977, p. 173).
No Capítulo V, os autores tratam da krigagem e avaliação de recursos in situ. O Teorema da Combinação das Estimativas de Krigagem, que permite fazer a krigagem de bloco a partir das krigagens de pontos, é demonstrado por Journel e Huijbregts (1978, p. 320-324). Além disso, vários programas de computador são apresentados, notadamente o programa KRI3D (Journel e Huijbregts, 1978, p. 369-385), que permite fazer a krigagem de blocos de um modelo tridimensional de blocos. Vale destacar o item V.C.3 em que Journel e Huijbregts (1978, p. 424-428) apresentam a estimativa de um quociente ou produto, bem como a incerteza associada. Merece destaque a expressão (6) que permite calcular a variância de um quociente (Q=A/B), como resultado da expansão de Taylor de segunda ordem.
![]()
O Capítulo VI estuda a influência da dimensão do bloco (tamanho e geometria) e da informação disponível, que podem ser traduzidos em termos das variâncias de estimativa e de dispersão, as quais são as principais contribuições da geoestatística às técnicas de avaliações minerais (Journel e Huijbregts, 1978, p. 445).
No Capítulo VII, a simulação de depósitos é apresentada como necessárias e complementares às estimativas locais e globais para fins de planejamento de uma nova mina ou uma nova seção de uma mina em operação (Journel e Huijbregts, 1978, p. 491).
O Capítulo VIII denominado introdução à geoestatística não linear, que não se limita à combinação linear dos dados disponíveis, mas como uma soma de suas funções. Entre esses métodos não lineares são apresentados a krigagem disjuntiva e a krigagem lognormal. Somente a krigagem lognormal será descrita neste livro, no Capítulo VII.
Referências:
Journel, A.G.; Huijbregts, Ch. J. Mining Geostatistics. Nova Iorque, Academic Press. 600p.
Retrospectiva da Geoestatística IV: Estimativa Geoestatística de Reservas Minerais (David, 1977)
Gosta de Geoestatística? Aprenda mais sobre seus conceitos:


Deixe um comentário
Você precisa fazer o login para publicar um comentário.