O que é a distribuição triangular?

Quando se sabe além do intervalo de variação da variável de interesse, um ponto dentro desse intervalo, pode-se usar a distribuição triangular para representação do modelo de probabilidade, bem como para fins de simulação estocástica conforme o método de Monte Carlo. Por exemplo, de acordo com o exemplo da porosidade de um reservatório desconhecido, há uma informação derivada de um poço exploratório, onde a porosidade foi determinada como sendo igual a 20%.

Na presença de dados esparsos, a distribuição triangular é frequentemente utilizada porque sua função densidade de probabilidade é claramente definida dentro dos limites inferior e superior, com uma densidade não uniforme (Leuangthong et al. 2008, p. 12). Segundo esses autores, essas propriedades tornam a distribuição triangular conveniente para quando a distribuição subjacente não é conhecida, além dos valores extremos e o valor mais provável.

Função densidade de probabilidade triangular

A função densidade de probabilidade da distribuição triangular é dada por (Evans et al., 1993, p. 149):

A esperança matemática e a variância da variável aleatória X com distribuição triangular são dadas por (Evans, 1993, p. 149):

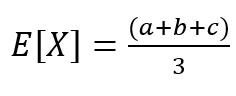
A função densidade de probabilidade e a distribuição de distribuição acumulada triangular são mostradas na Figura 1.

Observação: Este artigo foi atualizado a partir do item 2.7.8 do Capítulo 2 – Conceitos de probabilidade e estatística in Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. p. 12-45.

Referências:

Evans, M.; Hastings, N.; Peacock, B. 1993. Statistical distributions. New York, John Wiley & Sons. 170p.

Leuangthong, O.; Khan. K.D.; Deutsch, C.V. 2008. Solved problems in geostatistics. Hoboken, John Wiley & Sons. 208p.