Suavização da krigagem ordinária: correção

Como corrigir a suavização da krigagem ordinária?

No artigo anterior, vimos como se manifesta o efeito de suavização da krigagem ordinária, por meio da redução da variância, que se apresenta tanto no histograma como no variograma. Então, isso significa que a krigagem ordinária não proporciona precisão global. A reprodução da variabilidade espacial é importante para fins de inferência das propriedades do depósito mineral em estudo (população). Neste artigo, vamos ver como se pode fazer a correção do efeito de suavização da krigagem ordinária.

Como tratado em artigos anteriores, a incerteza associada à estimativa por meio da krigagem ordinária pode ser medida tanto pela variância de krigagem como pela variância de interpolação. A variância de krigagem não pode ser usada como uma medida de incerteza, mas tão somente como um índice da configuração espacial dos pontos de dados usados. Além disso, André Journel diz que a variância de krigagem é ilusória (prefácio do livro de Goovaerts, 1997, p. VIII). Por outro lado, a variância de interpolação é uma medida efetiva de incerteza, pois reflete a dispersão dos valores dos pontos de dados em relação à estimativa obtida por krigagem ordinária.

A título de rápida revisão do assunto, a estimativa por krigagem ordinária é feita por meio de uma expressão de média ponderada:

onde   são os pesos resultantes da solução de uma sistema de equações de krigagem ordinária.

A variância de interpolação pode ser calculada como uma média ponderada das diferenças ao quadrado entre os pontos de dados e o valor estimado (1):

  (2)

A variância de interpolação será sempre positiva se, e somente se, todos os pesos forem positivos. Para isso, há necessidade de se fazer uma correção dos pesos negativos.

A estimativa da krigagem ordinária (equação 1) está suavizada, ou seja, isso significa que os baixos valores são superestimados e os altos valores são subestimados. O ponto de partida para a correção do efeito de suavização está na determinação da incerteza associada, como se descreve a seguir.

Método de correção do efeito de suavização

Existem basicamente dois métodos propostos para a correção do efeito de suavização da krigagem ordinária. O primeiro proposto por Yamamoto (2005) se baseia na adição de um termo denominado erro de suavização derivado do processo de validação cruzada. O segundo método, proposto por Rezaee et al. (2011), usa a bem conhecida equação de transformação em estatística em que as estatísticas amostrais são usadas para corrigir a estimativa suavizada. Esse método será abordado em um futuro artigo.

O método proposto por Yamamoto (2005) e atualizado por Yamamoto (2007) parte de um processo de validação cruzada que permite obter o valor estimado para um ponto amostrado e daí calcular o erro, pois neste ponto se conhece o valor real. Na realidade, na validação cruzada se obtém, além da estimativa, o desvio padrão de interpolação. Dividindo-se o erro pelo desvio padrão de interpolação, tem-se uma nova variável aleatória denominada de número de desvios padrão de interpolação:

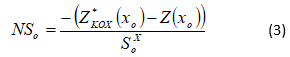
 é a estimativa obtida por krigagem ordinária da validação cruzada,  é o valor real e é o desvio padrão de interpolação no ponto amostral.

Observe-se que agora temos a nova variável   em todos os pontos de dados amostrais. Assim, essa variável pode ser interpolada em todos os nós da malha regular que se deseja obter  .
A variável de interesse   é também interpolada sobre os nós da malha regular. Assim, após a realização da validação cruzada e da krigagem ordinária, tem-se para cada nó da malha regular  e 

Esses valores são todos combinados para obtenção da variável corrigida da suavização, como segue:

 (4)

Portanto, trata-se em fazer um pós-processamento das estimativas obtidas por krigagem ordinária para correção do efeito de suavização, conforme a equação (4). Evidentemente, há outros detalhes que devem ser considerados para evitar a superestimativa ou subestimativa dos erros de suavização, os quais podem ser vistos em Yamamoto (2007).

Referências:

REZAEE, H. ; ASGHARI, O. ; Yamamoto, J.K. . On the reduction of the ordinary kriging smoothing effect. Journal of Mining & Environment, v. 2, p. 25-40, 2011.

YAMAMOTO, J. K.. Correcting the smoothing effect of ordinary kriging estimates. Mathematical Geology, v. 37, n.1, p. 69-94, 2005.

YAMAMOTO, J. K.. On unbiased backtransform of lognormal kriging estimates. Computational Geosciences, v. 11, p. 219-234, 2007