Como ajustar uma reta por meio da regressão robusta

Nem sempre, a reta de regressão dos mínimos quadrados é a que melhor se ajuda aos dados experimentais. Os conjuntos de dados podem estar alterados por simples erros de digitação ou erros causados por deriva instrumental. Neste artigo, vamos descrever o método da regressão robusta para o ajuste de uma reta baseada na minimização do desvio absoluto (Press et al. 1989, p. 595).

Este texto foi baseado no item 3.5.5: Regressão robusta, do Capítulo 3: Análise estatística do livro “Estatística, análise e interpolação de dados geoespaciais” (Yamamoto 2020, p. 80-83).

Quarteto de Anscombe

Para apresentar e ilustrar a regressão robusta, vamos usar os dados conhecidos como Quarteto de Anscombe, conforme a Tabela 1 (Anscombe, 1973, p. 19).

X1	Y1	X2	Y2	X3	Y3	X4	Y4
10	8,04	10	9,14	10	7,46	8	6,58
8	6,95	8	8,14	8	6,77	8	5,76
13	7,58	13	8,74	13	12,74	8	7,71
9	8,81	9	8,77	9	7,11	8	8,84
11	8,33	11	9,26	11	7,81	8	8,47
14	9,96	14	8,10	14	8,84	8	7,04
6	7,24	6	6,13	6	6,08	8	5,25
4	4,26	4	3,10	4	5,39	19	12,50
12	10,84	12	9,13	12	8,15	8	5,56
7	4,82	7	7,26	7	6,42	8	7,91
5	5,68	5	4,74	5	5,73	8	6,89

Regressão dos mínimos quadrados

A regressão dos mínimos quadrados pode ser influenciada pela existência de um ou mais pontos anômalos, por diversas razões, como, por exemplo, erro na digitação dos dados. Para ilustrar uma situação em que isso ocorre, seja a reta de regressão dos mínimos quadrados ajustada sobre os dados (Y3 por X3) do quarteto de Anscombe (1973, p. 19).

A regressão dos mínimos quadrados está representada na Figura 1.

Nesta figura, pode-se observar claramente que o ponto na coordenada X3=13 está deslocado dos demais pontos que desenham uma reta perfeita. Mas, a regressão dos mínimos quadrados é influenciada por este ponto anômalo.

Regressão robusta

A regressão robusta ajusta uma reta pela minimização dos desvios absolutos (Press et al. 1989, p. 595-597). Segundo esses autores, deve-se minimizar a função objetivo:

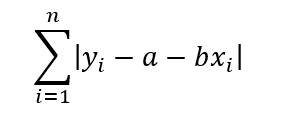
Esta equação implica que os coeficientes a e b da regressão dos mínimos quadrados são conhecidos, ou seja, o ponto de partida para a regressão robusta é justamente a realização da regressão dos mínimos quadrados.

A simplificação essencial vem do fato que a mediana c_M de um conjunto de números c_i é também o valor que minimiza a soma dos desvios absolutos (Press et al. 1989, p. 595):

Portanto, para um determinado valor de b, o valor de a que minimiza a função objetivo pode ser calculado como (Press et al. 1989, p. 595):

O parâmetro b_m, após determinação de a_m, pode ser calculado como (Press et al. 1989, p. 595):

A solução desta equação pode ser feita pelo método da bissecção (Press et al. 1989, p. 597). Mas, antes disso, determina-se o intervalo do coeficiente b, dentro do qual a função passe pelo zero. Trata-se de um processo iterativo, onde a cada iteração o valor do coeficiente b é calculado como a média entre os dois valores que limitam o intervalo.

Assim em cada iteração, o valor de am também é determinado e dessa forma até que a diferença entre dois valores sucessivos de b esteja dentro de um erro aceitável. Detalhes do método da bissecção podem ser vistos em Hamming (1973, p. 62-63).

Fazendo a regressão robusta para esses dados (Y3 por X3), obtém-se a reta mostrada na Figura 2C, que representa melhor os dados disponíveis. Esta figura apresenta também os resultados das demais regressões para os quatro conjuntos de pontos, onde se pode verificar que para os conjuntos (Y1 por X1) e (Y4 por X4), as regressões dos mínimos quadrados e robusta são absolutamente iguais.

A regressão do conjunto (Y2 por X2) apresenta resultados ligeiramente diferentes entre os dois métodos. Os dados do quarteto de Anscombe (1973) têm sido usados para demonstrar a importância dos gráficos em estatística. Por exemplo, na Figura 2B os pontos descrevem uma parábola e, portanto, a reta não seria a melhor escolha para definir a relação entre as variáveis Y2 e X2. Por outro lado, a regressão para os conjuntos de pontos da Figura 2D foi definida por apenas um ponto, como foi ressaltado por Anscombe (1973, p. 19).

Os dados do quarteto de Anscombe (1973) foram gerados de tal forma que todas as estatísticas fossem iguais e, consequentemente, as regressões dos mínimos quadrados, como se pode verificar na Tabela 2.

Par	X	Y	Var[X]	Var[Y]	Cov(X,Y)	a	b
X1xY1	9	7,500909	10	3,752063	5,000909	3,000091	0,500091
X2xY2	9	7,500909	10	3,752390	5,000000	3,000909	0,500000
X3xY3	9	7,500000	10	3,747836	4,999727	3,002455	0,499727
X4xY4	9	7,500000	10	3,762045	5,007273	2,993455	0,500727

Considerações finais

Este artigo tratou da apresentação da regressão robusta, que é indicada para dados com a existência de pontos anômalos. Na ausência de pontos anômalos, as regressões dos mínimos quadrados e robusta produzem resultados muito próximos entre si, como se pode verificar nas Figuras 2A e 2D.

Referências bibliográficas

Anscombe, F.J. 1973. Graphs in statistical analysis. American Statistician, v. 27, p. 17-21.

Hamming, R.W. 1973. Numerical methods for scientists and engineers. New York, Dover Publications, Inc. 721p.

Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. 1989. Numerical recipes in Pascal. New York, Cambridge University Press. 759p.

Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 308p.

Próximo artigo

Os dois próximos artigos irão tratar da transformação de dados, que serão derivados do Capítulo 4: Transformação de dados (Yamamoto, 2020, p. 90-99). A transformação de dados é uma técnica comumente aplicada no tratamento de variáveis com distribuições assimétricas positivas como, por exemplo, a distribuição de metais nobres (ouro, prata, platina etc.).