Probabilidade Condicional: Fórmula de Bayes

A colocação do problema, conforme segue, foi baseada inteiramente em Caers (2011, p. 19). A probabilidade de encontrar diamante em uma região é uma probabilidade incondicional. Mas, à medida que mais dados se tornam disponíveis (por exemplo, a rocha é kimberlítica e granadas são encontradas), a probabilidade de um evento irá aumentar ou diminuir, cuja magnitude é governada pela fórmula de Bayes (Caers, 2011, p. 19).

Sejam dois eventos A e B, com P(A) > 0, denomina-se probabilidade condicional P(B|A) a probabilidade de B dado que A ocorreu (Spiegel et al. 2013, p. 7). Um valor de probabilidade calculado sob a suposição que um outro evento tenha ocorrido é chamado de probabilidade condicional, segundo Lapin (1998, p. 79).

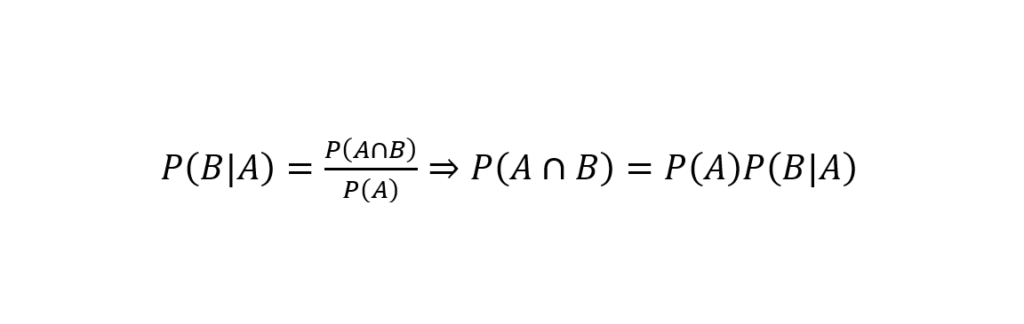
Como a conjunção é comutativa para quaisquer eventos A e B (Downey, 2012, p. 3), ou seja:

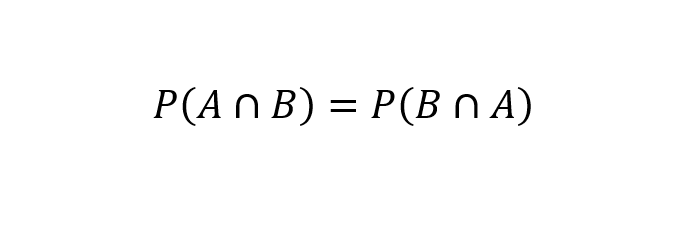
            Pode-se escrever:

            Dividindo-se (1) por (2), tem-se a fórmula de Bayes (Downey, 2012, p. 4):

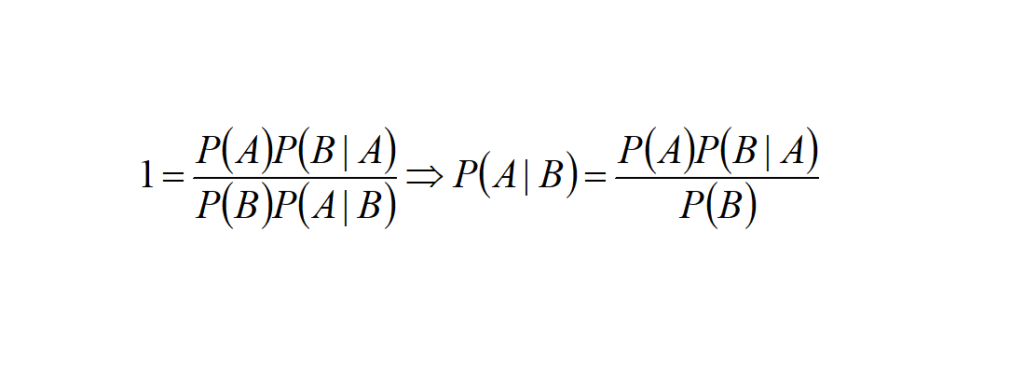
A regra de Bayes é um método rigoroso para interpretação de evidência no contexto de experiência prévia ou conhecimento (Stone, 2013, p. 1).

Qual é a probabilidade de um depósito de diamante ser economicamente viável?

Para ilustrar uma aplicação prática da Fórmula de Bayes, considere-se o exemplo dado por Caers (2011, p. 20), com adaptações livres desse Autor. Um geólogo que trabalhou por 30 anos na indústria do diamante sabe da sua experiência que 1/10 dos depósitos que estudou são economicamente viáveis. Agora, ele precisa avaliar um novo depósito e calcular a probabilidade que esse depósito é viável. Ele sabe que a probabilidade de a granada ser maior que 5 ppm em depósitos viáveis é 4/5, enquanto para aqueles não viáveis é apenas 2/5. Então, nesse novo depósito, o conteúdo de granada é 6,5 ppm.

Para a solução desse problema, sejam os seguintes eventos: E₁ = o depósito é viável; E₂ = o depósito não é econômico; F₁ = teor de granada é > que 5 ppm; F₂ = o teor de granada é £ 5 ppm (Caers, 2011, p. 20).

Pela fórmula de Bayes, deve-se determinar a probabilidade que o depósito é viável, dado que o teor de granada é maior que 5 ppm, isto é:

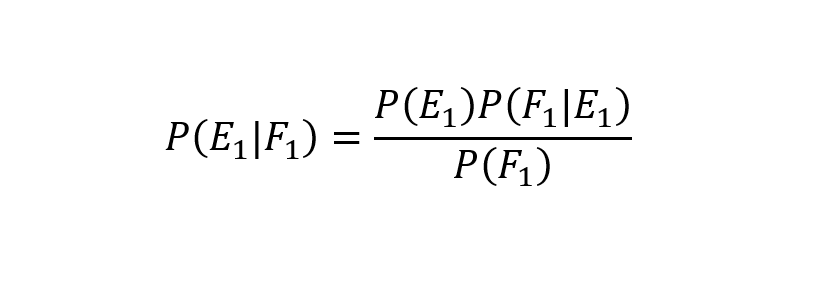
Na verdade, há necessidade de se determinar P(F₁), o teor de granada que pode ser maior que 5 ppm, tanto em depósitos viáveis como naqueles não econômicos. Nesse caso, usamos a Lei das Probabilidades Totais (Devore, 2000, p. 81), que diz que se existem duas maneiras exclusivas que algo pode acontecer, então se pode somar as probabilidades, como a expressão a seguir (Downey, 2012, p. 6). Desta forma, para calcular P(F₁), soma-se as probabilidades, conforme:

Segundo Caers (2011, p. 20), sabe-se que a probabilidade a priori P(E₁)=1/10 e, portanto, P(E₂)=9/10. Também, tem-se que P(F₁|E₁)=4/5 e P(F₁|E₂)=2/5. Logo, P(F₁) pode ser calculada como:

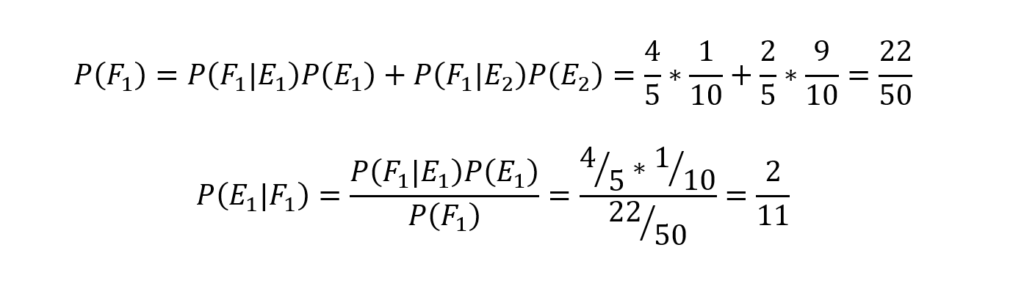
Conclusão

Portanto, sabendo que o teor de granada é maior que 5 ppm, a chance de o depósito ser economicamente viável é quase duas vezes mais (0,18 em relação a 0,10). De fato, a razão da probabilidade a posteriori sobre a probabilidade a priori é 1,81 (Caers, 2011, p. 20).

Observação: este artigo foi derivado Yamamoto (2020) “Conceitos de probabilidade e estatística”.

Referências bibliográficas

Caers, J. 2011. Modeling uncertainty in the Earth Sciences. Sussex, Wiley-Blackwell. 229p.

Devore, J.L. 2000. Probability and statistics for engineering and the sciences. Pacific Grove, Duxbury. 775p.

Downey, A.B. 2012. Think Bayes. Bayesian statistics made simple. Needham, Green Tea Press. 195p.

Lapin, L.L. 1998. Probability and statistics for modern engineering. Prospect Heights, Waveland Press. Inc. 810p.

Spiegel, M.T.; Schiller, J.J.; Srinivasan, R.A. 2013. Probability and Statistics. New York, Mc Graw Hill. 424p.

Yamamoto, J.K. 2020. Conceitos de probabilidade e estatística. In: Yamamoto, J.K. Estatística, análise e interpolação de dados geoespaciais. São Paulo, JK Yamamoto. 355p. Lançamento para julho/agosto de 2020.