Como posso calcular a moda de minha distribuição de frequências?

A moda, por definição, é o valor mais frequente da distribuição de frequências. Para variáveis discretas, a moda é facilmente definida pela simples verificação da tabela de frequências, sendo a moda atribuída ao tipo que tem maior frequência. Neste artigo vamos ver como calcular a moda da distribuição de frequências.

Entretanto, para variáveis contínuas, nem sempre isso é possível, pois os valores amostrados podem simplesmente não se repetir e, assim, todos os dados apresentarem frequências iguais a 1/N. Por que 1/N?

O Conceito de Probabilidade

Então, antes de calcular a moda, vamos revisar o conceito de probabilidade. Se o espaço amostral é composto por um número finito de realizações a₁, a₂, … , a_N, tem-se (Spiegel et al. 2013, p. 6):

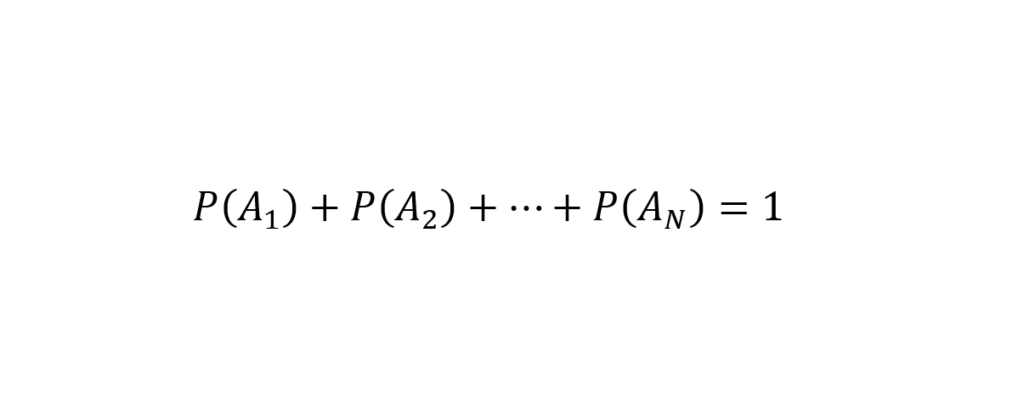
Assumindo probabilidade iguais para todas as realizações ou eventos simples, tem-se (Devore, 2000, p. 64; Spiegel et al. 2013, p. 6):

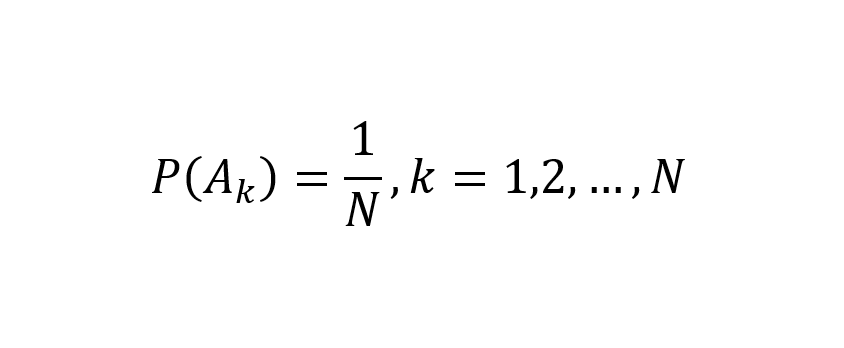
A melhor opção seria analisar o histograma, sabendo-se que a moda estará contida no intervalo de classe de maior frequência. Isto significa calcular a moda a partir de dados agrupados. Existem dois métodos para determinação da moda a partir de dados agrupados (Francis, 2004, p. 117):

• Interpolação numérica;
• Determinação gráfica.

A interpolação da moda pode ser feita com base na seguinte fórmula (Francis, 2004, p. 118):

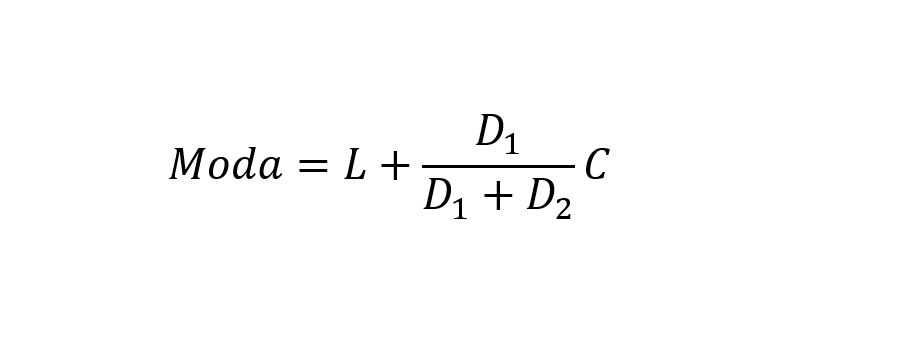
onde L é o limite inferior da classe modal; C é a largura da classe modal; D₁ é a diferença entre a maior frequência e a frequência da classe imediatamente anterior; D₂ é a diferença entre a maior frequência e frequência da classe imediatamente seguinte.

Interpretação Gráfica da Moda

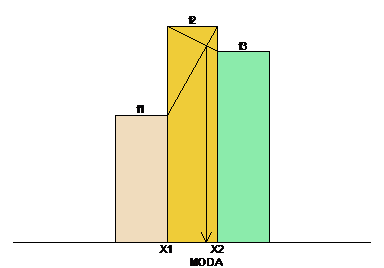
A moda também pode ser determinada graficamente, como ilustrada na Figura 1, por meio do ponto de intersecção entre as duas retas (Francis, 2004, p. 119). Esta construção gráfica permite obter a moda com uma boa precisão, pois ela é influenciada pela frequência da classe anterior ou posterior. No caso da Figura 1, a frequência f3 desloca a moda para direita.

Sejam três conjuntos de pontos de dados, denominados: positive100.csv, simetrica100.csv e negative100.csv. A partir de seus histogramas, localizou-se as classes modais, ou seja, as classes de maior frequência.

Identificadas as classes modais, pode-se determinar a moda gráfica ou numericamente, pois essas aproximações são absolutamente equivalentes. A Figura 2 exemplifica o procedimento gráfico para determinação das modas das distribuições de frequências em estudo.

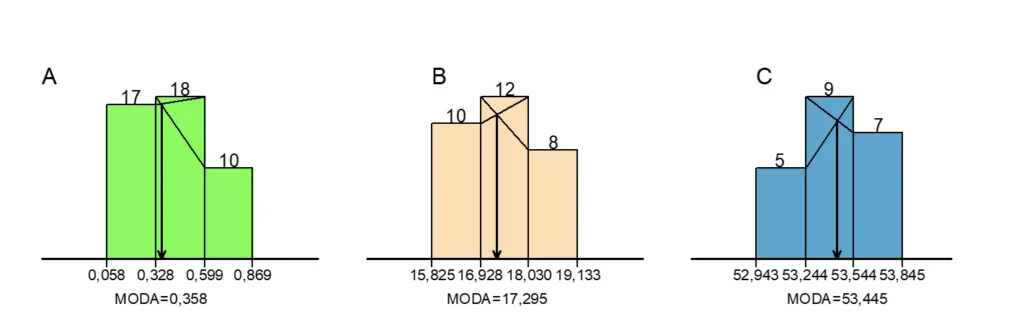
Como se pode observar na Figura 2, a determinação da moda deve levar em consideração a maior frequência imediatamente anterior ou posterior à classe modal, pois ela desloca a moda nessa direção.

Analiticamente, pode-se determinar a moda, conforme os resultados apresentados para as distribuições positive100.csv, simetrica100.csv e negative100.csv, respectivamente.

Conclusão

Como se pode verificar, a atribuição da moda como o ponto médio da classe modal é uma aproximação que pode resultar em erro, principalmente quando a distribuição de frequências apresentar assimetria positiva.

No próximo artigo, apresentaremos um script para calcular a moda usando a linguagem R. Aguarde!

Observação: este artigo foi derivado Yamamoto (2020) “Análise estatística”.

Referências bibliográficas:

Devore, J.L. 2000. Probability and statistics for engineering and the sciences. Pacific Grove, Duxbury. 775p.

Francis, A. 2004. Business mathematics and statistics. Hampshire, South-Western. 665p.

Spiegel, M.T.; Schiller, J.J.; Srinivasan, R.A. 2013. Probability and Statistics. New York, Mc Graw Hill. 424p.

Yamamoto, J.K. 2020. Análise estatística. In: Yamamoto, J.K. Estatística, análise e interpolação de dados geoespaciais. São Paulo, JK Yamamoto. 355p. Lançamento para julho/agosto de 2020.