Na distribuição lognormal dos dados de ouro, os poucos valores obtidos em um bloco de minério representam somente uma pequena parte de um número virtualmente infinito de valores que podem ser obtidos por amostragem repetida
Krige, 1951, p. 16
Introdução
Este artigo reflete em sua íntegra, com algumas modificações, o conteúdo do item 2.7.6, do Capítulo 2: Conceitos de probabilidade e estatística do nosso livro: Estatística, Análise e Interpolação de dados geoespaciais (Yamamoto, 2020).
Como mencionado no artigo anterior, este texto tem por objetivo apresentar como os assuntos são tratados no referido livro.
Neste artigo, vamos abordar a distribuição lognormal, que tem uma grande importância na análise de variáveis que apresentam uma assimetria positiva, como, por exemplo, a ocorrência de fenômenos raros (terremotos) e a distribuição de metais nobres (ouro, prata etc.). As demais distribuições de probabilidade, discretas (binomial e Poisson) e contínuas (exponencial, chi-quadrado, F, t de Student, uniforme e triangular), são apresentadas no nosso livro Yamamoto (2020, p. 21-40).
Distribuição lognormal
Muitas das distribuições encontradas em geologia não são simétricas, mas geralmente assimétricas positivas, onde altos teores ocorrem além do intervalo considerado em distribuições normais, que podem converter mineralizações em corpos de minério (Wellmer, 1998, p. 53).
Esses altos teores não podem ser ignorados porque eles indicam a localização das zonas de altos teores que são essenciais durante a exploração mineral de um depósito (Wellmer, 1998, p. 53).
A distribuição lognormal é uma distribuição simples que pode ser usada para variáveis não negativas com assimetria positiva (Rossi e Deutsch, 2014, p. 14). A assimetria positiva significa que a cauda da distribuição está sobre os valores altos, onde inclusive podem ocorrer valores mais altos que aqueles amostrados. Distribuições assimétricas sem um limite superior (0 < x < ∞) estão associadas com trabalho ou entrada de energia em um sistema, como, por exemplo, magnitudes de terremotos e impactos de meteoritos que não têm limite máximo (Borradaile, 2003, p. 121).
A Figura 1 ilustra uma distribuição de frequências com assimetria positiva. Geralmente, essa distribuição é caracterizada pela ocorrência de uma grande quantidade de valores baixos e uma quantidade muito pequena de valores altos ou muito altos. Usualmente, essa distribuição está associada à ocorrência de fenômenos raros, tais como magnitude de terremotos, teores de ouro em uma mina, cheias de rios e altura dos edifícios em Nova York (Koch e Link, 1970, p. 215).
Segundo Krige (1951, p. 15), a distribuição lognormal deve compreender uma mistura de valores variando teoricamente do zero ao infinito. Na distribuição lognormal dos dados de ouro, os poucos valores obtidos em um bloco de minério representam somente uma pequena parte de um número virtualmente infinito de valores que podem ser obtidos por amostragem repetida (Krige, 1951, p. 16).
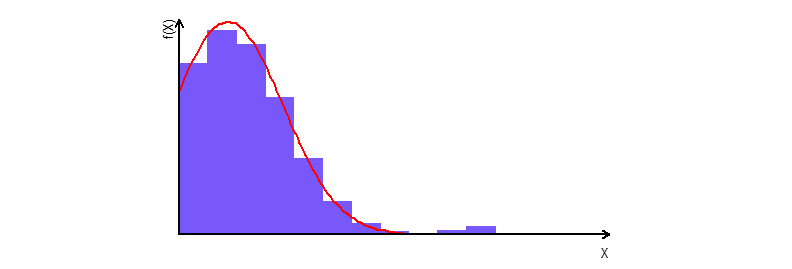
A distribuição lognormal é uma distribuição contínua caracterizada pela propriedade que os logaritmos dos valores seguem uma distribuição normal (Koch e Link, 1970, p. 213, Isaaks e Srivastava, 1989, p. 15). Mas, isso não é suficiente, pois há necessidade de se entender como se origina a distribuição lognormal.
No artigo anterior foi demonstrado por meio do Teorema do Limite Central que uma variável aleatória resultante da soma de n variáveis aleatórias no limite, ou seja, quando n tende ao infinito, essa variável segue uma distribuição normal. Da mesma forma, se X é o produto de n variáveis aleatórias (X=X1X2…Xn), fazendo Y=lnX, então Y segue uma distribuição normal (Haan, 1977, p. 106):
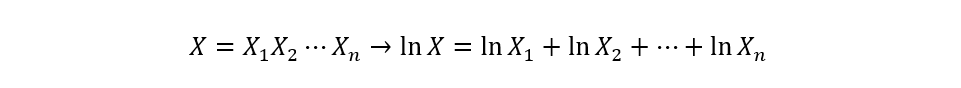
Como Xi são variáveis aleatórias, ln(Xi) também são variáveis aleatórias e, igualmente, lnX como soma de n variáveis aleatórias segue uma distribuição normal (Haan, 1977, p. 106-107). Em termos gerais, dada uma variável aleatória X e função g(x), a expressão (segundo Hsu, 2014, p. 149):
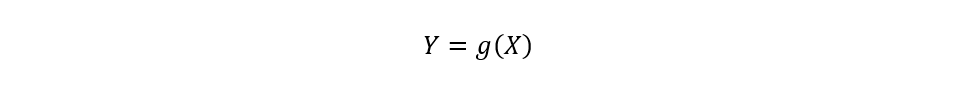
define uma nova variável aleatória Y.
A distribuição lognormal é importante por causa de sua história em estatística espacial e geoestatística (Rossi e Deutsch, 2014, p. 14).
Função densidade de probabilidade lognormal
Levando em consideração a mudança de variável, a função densidade de probabilidade da distribuição lognormal pode ser desenvolvida a partir da seguinte relação (Agterberg, 1974, p. 194; Haan, 1977, p. 107 e Abramowitz e Stegun, 1972, p. 69):
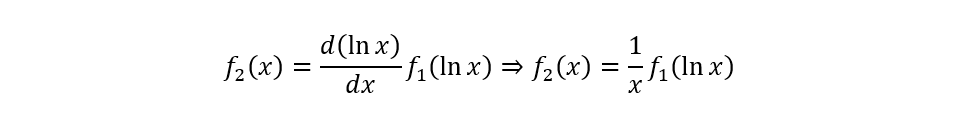
Onde, o segundo termo f1(ln x) é a função densidade de probabilidade normal. Assim, a função densidade de probabilidade lognormal fica (Agterberg, 1974, p. 194):
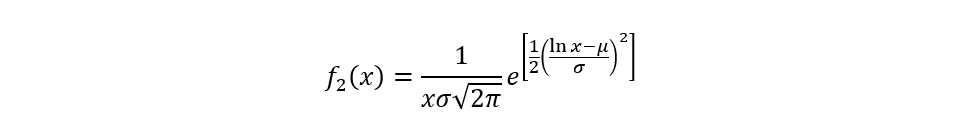
Onde µ e σ são respectivamente a média e o desvio padrão dos logaritmos dos valores.
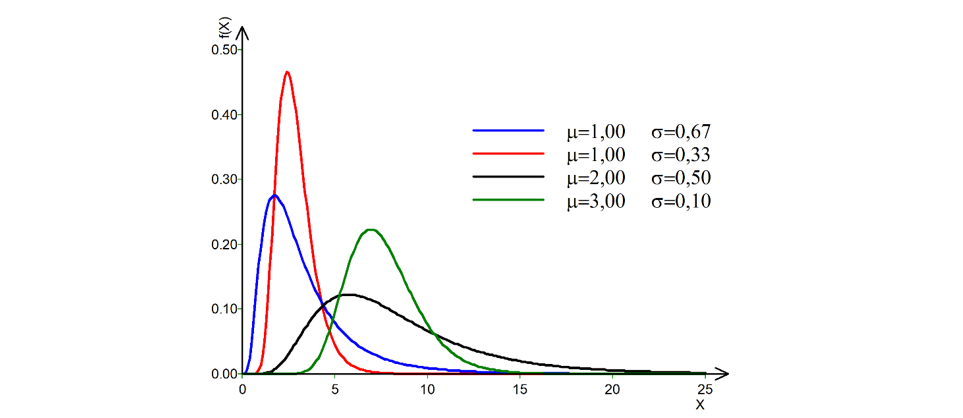
A Figura 2 apresenta algumas funções densidade de probabilidade para distribuições lognormais com parâmetros variáveis. A assimetria aumenta com o desvio padrão dos logaritmos.
Considerações finais
Na mineração do ouro, o entendimento da distribuição lognormal é de suma importância, pois os teores máximos amostrados nos programas de exploração mineral representam somente uma pequena parte de um número virtualmente infinito de valores que podem ser obtidos por amostragem repetida, como foi muito bem observado por Krige (1951, p. 16).
Isso significa que é perfeitamente possível que teores maiores que aqueles máximos observados sejam obtidos na fase de lavra do depósito mineral.
O tratamento dos dados de ouro para avaliação de recursos minerais deve passar pela sua transformação para evitar a influência dos poucos valores altos na estimativa de regiões com valores baixos. Krigagem lognormal e krigagem multiGaussiana são as técnicas indicadas para avaliação dos recursos de ouro. Deve-se lembrar, contudo, que a transformada reversa deve ser feita levando em consideração a suavização introduzida pela krigagem.
Lembrando que este artigo reproduz integralmente, com alguns ajustes, o conteúdo do item 2.7.6, do Capítulo 2: Conceitos de probabilidade e estatística do nosso livro: Estatística, Análise e Interpolação de dados geoespaciais (Yamamoto, 2020).
Adquira o livro e tenha acesso a todo esse conteúdo exclusivo!
Referências bibliográficas
Abramowitz, M.; Stegun, I.A. 1972. Handbook of mathematical function with formulas, graphs, and mathematical tables. New York, Dover Publications Inc. 1046p.
Agterberg, F.P. 1974. Geomathematics: Mathematical background and Geo-Science Applications. Amsterdam, Elsevier. 596p.
Borradaile, G. 2003. Statistics of earth science data. Heidelberg, Springer. 351p.
Haan, C.T. 1977. Statistical methods in hydrology. Ames, The Iowa State University Press. 378p.
Hsu, P.H. 2014. Probability, random variables, and random processes. New York, McGraw Hill. 422p.
Isaaks, E.H.; Srivastava, R.M. 1989, Applied geostatistics, New York, Oxford University Press. 561p.
Koch, G.S.; Link, R.F. 1970. Statistical analysis of geological data. New York, Dover Publications Inc. Vol. I. 375 p.; Vol. II. 438p.
Krige, D.G. 1951. A statistical approach to some mine valuation and allied problems on the Witwatersrand. M. Sc. Thesis presented to the University of Witwatersrand. 136p.
Rossi, M.; Deutsch, C.V. 2014. Mineral resource estimation. Dordrecht, Springer. 332p.
Wellmer, F.W. 1998. Statistical evaluations in exploration for mineral deposits. Heidelberg, Springer. 379p.
Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 308p.
Próximo artigo
Os dois próximos artigos irão abordar itens do Capítulo 3: Análise estatística do livro: Estatística, análise e interpolação de dados geoespaciais (Yamamoto, 2020, p. 46-89).


Deixe um comentário
Você precisa fazer o login para publicar um comentário.