Distribuição de frequências

O que é uma distribuição de frequências?

O primeiro passo no estudo estatístico de uma variável aleatória consiste na obtenção da distribuição de frequências, ou seja, como os valores se encontram distribuídos dentro do intervalo de variação. Na verdade, a distribuição de frequências é usada para organizar as observações, por meio da classificação, agrupamento e calculando a média para sumariar a informação numérica (Koch e Link, 1970, p. 30-Vol. I).

Conhecido o intervalo de variação entre Xmin e Xmax, deve-se decidir o número de classes (nc), nas quais serão contadas as frequências de ocorrência dos valores. O tamanho da classe (tc) pode assim ser calculado:

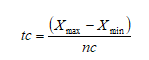
Com relação ao número de classes, este não deve ser tão pequeno quanto dois ou tão grande quanto o número de dados. Nesse caso cada dado vai ser representado pela sua frequência individual. Em geral, o número de classes deve ser uma pequena porcentagem do número total de dados.

Existem algumas regras que permitem calcular o número de classes: raiz quadrada (Kennedy, 2015, p. 161) e as regras de Sturge e de Rice (Basu e Basu, 2016, p. 30-31):

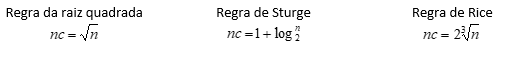
A título de ilustração, a Tabela 2 apresenta o número de classes para alguns valores escolhidos.

Tabela 2: Número de classes conforme as regras da raiz quadrada, Sturge e de Rice.

Como se verifica nesta tabela, para um número pequeno de dados (menor que 50), as diferentes regras resultam em praticamente no mesmo número de classes. Entretanto, quando o número de dados aumenta, tanto a regra da raiz quadrada como a de Rice mostram valores muito altos.

Assim, a regra de Sturge parece ser mais adequada, pois mantém um número de classes razoável para estudo de uma distribuição de frequências. Por exemplo, considere-se que um depósito mineral foi amostrado na fase preliminar da pesquisa por 500 pontos. Em seguida, o mesmo depósito mineral foi detalhado com pesquisa adicional e passou a ter 1000 pontos.

Pela regra de Sturge, o número de classes passaria de 10 para 11, ou seja, praticamente o mesmo valor. Muito provavelmente, na fase preliminar da pesquisa os 500 pontos já forneceriam a informação do intervalo de variação dos valores da variável de interesse. Considerando que a pesquisa adicional não alteraria muito o intervalo de variação, não haveria justificativa para um aumento no número de classes.

Para ilustrar os procedimentos da análise estatística, considere-se três amostras aleatórias estratificadas extraídas de conjuntos completos denominados normal.txt, positiva.txt e negativa.txt (Tabela 1).

Como há 49 pontos de dados, o número de classes pela regra de Sturge é igual a sete. O intervalo de variação da amostra extraída de normal.txt é de 5,23 a 24,91. Assim, o tamanho da classe pode ser calculado como:

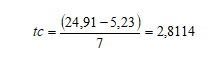
Com isso, pode-se determinar a distribuição de frequências da variável Zgauss.

Referências:

Basu, A.; Basu, S. 2016. A users’s guide to business analytics. Boca Raton, CRC Press. 383p.

Koch, G.S.; Link, R.F. 1970. Statistical analysis of geological data. New York, Dover Publications Inc. Vol. I. 375 p.; Vol. II. 438p.

Kennedy, M. 2015. Practical petrophysics. Amsterdam, Elsevier. 403p.

Gostou do artigo? Compartilhe!