Introdução
A validação de bases de dados de sondagens de campanhas distintas ou entre sondagens de diferentes tipos constitui um problema recorrente ao geólogo ou engenheiro de minas envolvido na avaliação de recursos minerais. A questão principal está relacionada ao suporte amostral, que se refere ao tamanho, forma e volume da amostra.
A regularização deixa as amostras com comprimentos iguais, mas não é condição suficiente se o volume amostrado entre diferentes métodos de sondagem não for constante. Observe-se que a variância é inversamente proporcional ao volume, tendo-se em conta que a relação volume-variância é constante.
Como fazer a validação de bancos de dados para a avaliação de recursos minerais
A validação de sondagens de diferentes métodos e campanhas não é uma atividade simples.
Atualmente, deve-se procurar pares de furos próximos ou obter furos gêmeos para estudar a correlação entre valores amostrados em intervalos geologicamente correspondentes. No caso de diferentes métodos de sondagem, que são combinados para a pesquisa mineral de um depósito, a validação é feita pela comparação dos teores de intervalos amostrados de furos gêmeos, que são feitos próximos um do outro.
Então, a decisão sobre a compatibilidade entre os resultados de diferentes métodos é baseada no coeficiente de correlação entre os teores representados em um diagrama de dispersão. A critério do responsável pela pesquisa mineral, o nível de correlação mínimo é estabelecido e a validação das sondagens pode ser decidida.
Na prática, a correlação não é muito alta,
devido à natureza estocástica da variável geológica. Além disso, nem sempre é possível fazer um furo muito próximo do outro, por problemas técnicos. Por exemplo, há relatos de rompimento da parede do furo quando uma sondagem por circulação reversa é feita próxima de um furo pronto por sondagem rotativa a diamante. Os pares de furos gêmeos, a serem representados no diagrama de dispersão, devem ter correspondência litológica e estrutural.
Dessa forma, pode-se comparar teores de pares de furos gêmeos
por meio da medida do coeficiente de correlação linear de Pearson. Entretanto, esta estatística é local, pois diz respeito a uma localização específica no depósito mineral. Assim, propõe-se o uso de uma estatística global para validação de sondagens feitas por diferentes métodos. Trata-se da curva acumulativa, que representa a distribuição de frequências acumuladas de todos os pontos de dados.
Assim, pode-se representar duas ou mais distribuições de frequências acumuladas em apenas um gráfico e, dessa forma, comparar essas distribuições visualmente, verificando o quão próximas estão as distribuições, ou quantitativamente, por meio das estatísticas descritivas: média, desvio padrão, coeficiente de variação e os quartis da distribuição acumulada.
Essa validação é possível se os teores obtidos por diferentes métodos ou de campanhas distintas estiverem regularizados em intervalos constantes, seja por bancadas ou down-the-hole.
Se a regularização não for considerada, pode-se introduzir uma componente adicional de variação, que não é desejável, dificultando a tomada de decisão. Essas curvas representam as funções de distribuição acumulada, das quais se pode determinar a probabilidade que o valor da variável é menor que um valor de referência:
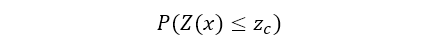
Na verdade, pode-se usar a expressão seguinte que descreve uma função de distribuição acumulada conjunta, que caracteriza o depósito mineral em termos de sua distribuição de frequências (Matheron, 1976, p. 13):
![]()
Considerando conjuntos distintos de sondagens, idealmente se procura a seguinte relação de igualdade para validação dos mesmos:
![]()
Fazendo isso para vários teores de referência, pode-se ter funções de distribuição acumulada conjuntas, que permitem verificar se as bases de dados são equivalentes.
A Figura 1 representa as sondagens feitas por rotativa a diamante (DD) e por circulação reversa (RC).

Percebe-se que as distribuições acumuladas mostram boa correlação e aderência.
Entretanto a correlação visual entre as curvas não é suficiente para fins de validação de diferentes métodos. Deve-se fazer a comparação quantitativa por meio das estatísticas descritivas dos dois conjuntos de dados, como se apresenta na Tabela 1.

Como se pode verificar, existe uma grande diferença entre as médias amostrais, apesar da dispersão ser praticamente a mesma (2,296 contra 2,310).
Observe-se que, pelo teorema da amostragem, a média amostral deve se aproximar da média populacional. Nesse sentido, se houver uma pequena diferença entre as médias, pode-se proceder à correção da média, tendo em vista que:

Ou seja, pode-se tanto multiplicá-la por uma constante ou adicioná-la para correção da média. A primeira forma de correção também altera a variância, pois:

Lembrando que a adição de uma constante não altera a média, conforme:

Dessa forma, como as dispersões estão próximas entre si, a correção ideal seria pela adição de uma constante igual a K=7,532-7,142=0,390 para os dados da sondagem por circulação reversa. Observe-se que estamos usando as sondagens rotativas a diamante como referência. As estatísticas descritivas da distribuição de frequências após aplicação da correção estão listadas na Tabela 2.

Comparando os resultados com os dados originais da Tabela 2, verifica-se que a média foi corrigida, sem alteração do desvio padrão. Contudo, as demais estatísticas, principalmente os quartis foram todos deslocados à direita pela constante (K=0,390).
Os resultados da aplicação da soma de uma constante (K=0,390) aos dados das sondagens por circulação reversa estão representados na Figura 3.

Como se pode observar, a soma de uma constante não é suficiente para deixar as distribuições exatamente iguais. Nesse sentido, pode-se aplicar uma função de transformação para ajustar toda a distribuição de frequências acumuladas por meio de um algoritmo inédito. Essa transformação garante uma aderência mínima de 99% em relação à distribuição de referência.
Trata-se do programa GKY
O GKY foi desenvolvido pela Geokrigagem, totalmente escrito em linguagem Delphi 2010 e compatível com sistemas operacionais Windows. A janela inicial do programa está apresentada na Figura 4, onde se pode ver os histogramas das duas distribuições, bem como o histograma resultante da transformação dos dados de RC para DD. Comparando-se as estatísticas da variável após transformação com as estatísticas da variável de referência, verifica-se uma aderência completa, que também pode ser notada visualmente (Figura 5).
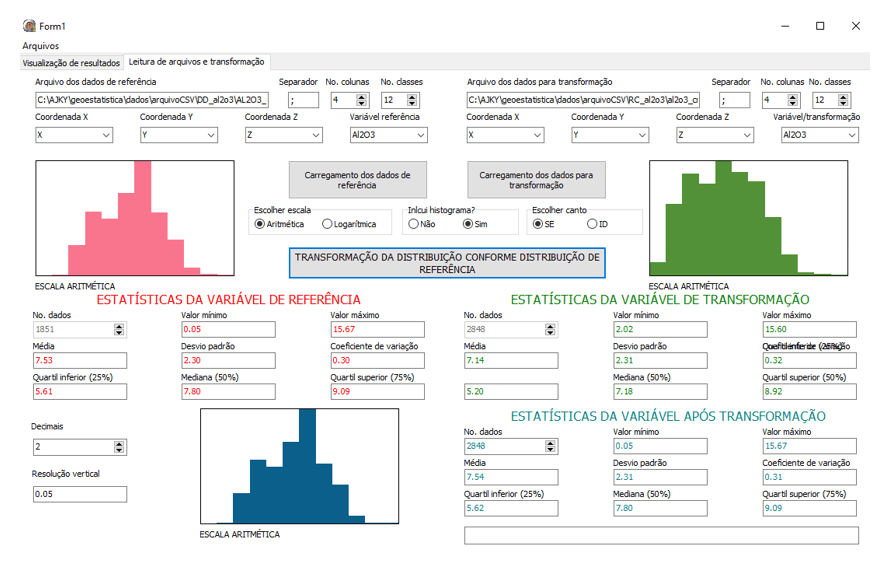
A Figura 5 mostra uma excelente aderência dos dados transformados em relação à distribuição de referência. Os diagramas P-P e Q-Q confirmam a excelente aderência dos dados transformados em relação à distribuição de referência. O diagrama de dispersão ilustra uma relação quase linear entre os dados (antes da transformação) e após.

A Geokrigagem disponibilizará aos interessados umaversão demo, sem custo. Apesar de fazer as transformações de dados, nesta versão demo, o usuário não conseguirá salvar os dados corrigidos. Caso o programa completo seja de interesse do usuário, pede-se entrar em contato por meio do e-mail: contato@geokrigagem.com.br
Considerações finais
A validação de campanhas distintas de sondagens ou de diferentes tipos de sondagens, desde que regularizados em intervalos iguais, torna-se possível pela comparação das distribuições de frequências acumuladas. Muitas vezes, a aderência entre as curvas acumulativas não é total. Nesses casos, é necessária a correção por meio da aplicação da função de transformação disponível no programa GKY.





