Regularização Down-The-Hole de amostras com observações qualitativas

As variáveis discretas

Dando continuidade ao assunto, falaremos das variáveis discretas – as quais também precisam de um tratamento prévio com o objetivo de deixar as observações com um suporte constante. Os artigos anteriores trataram da regularização de variáveis contínuas, por meio da média ponderada (equação 1), conforme Yamamoto e Rocha (2001, p. 4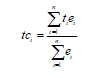1):

 

 (1)

 

 

Entretanto, as variáveis discretas não podem ser manipuladas diretamente por meio da equação (1), mas apenas após a sua transformação em funções indicadoras (Rivoirard, 1994, p. 16).

A regularização neste caso

Na verdade, o objetivo da regularização de variáveis discretas é a modelagem geológica ou geotécnica de um maciço rochoso. Nesse caso, não faz sentido falar em regularização por bancada, mas sim na regularização do furo em trechos de comprimento constante, a partir da boca do furo.

A regularização down-the-hole também pode ser aplicada para a modelagem geoestatística de recursos minerais, quando a lavra não se der pelo método tradicional de bancadas a céu aberto.

O tratamento matemático

Ao invés da equação da média ponderada (equação 1) usa-se a observação mais frequente. Como se verá nas postagens futuras, o tratamento matemático de variáveis discretas ou categóricas é feito por meio da transformação em funções indicadoras. Considerando uma variável categórica (tipo de rocha, cor da rocha, grau de alteração, grau de faturamento etc.) composta por K tipos, pode-se fazer a codificação indicadora conforme segue (Yamamoto et al., 2012, p. 147):

(2)

A codificação binária segundo a equação (2) é mutuamente exclusiva, pois se uma determinada litologia está presente no ponto x, significa que as funções indicadoras correspondentes às demais litologias serão iguais a zero.

Considere-se um trecho composto por n intervalos de-para, para o qual se deseja saber o tipo mais frequente. Assim, calcula-se a frequência para o k-ésimo tipo:

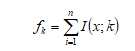 (3)

Repetindo para todos os K tipos, pode-se determinar o tipo que apresenta a frequência máxima como:

 (4)

A Tabela 1 apresenta os dados de um furo inclinado com intervalos de-para contendo dados de litologia. Portanto, a variável categórica é litologia, que é composta por três tipos (1, 2 e 3). O objetivo é mostrar na prática como se realiza a regularização de dados discretos.

Tabela 1: Log de um furo inclinado com descrição da litologia.

Como mencionado anteriormente, não tem sentido fazer a regularização por bancadas, pois a modelagem geológica não será feita com base na unidade de mineração. Assim, faz-se a regularização por intervalo constante a partir da cota da boca do furo.

Representações nas figuras

Para esse exemplo foi escolhido um intervalo de 5 m. A Figura 1 representa o furo inclinado com suas litologias, bem como o resultado da regularização para três intervalos escolhidos (#3, #5 e #7). Considere-se o furo nas coordenadas (180, 140 e 104), com azimute 130º e inclinação de 57,529º.

Figura 1: Representação do furo inclinado com as litologias e o
resultado da regularização, com destaque para o cálculo do
tipo mais frequente para três intervalos selecionados.

Como se pode verificar nas caixas destacadas (Figura 1), a litologia é transformada em função indicadora. Como a variável categórica é composta por três tipos, tem-se três vetores que representam as funções indicadoras de cada tipo.Em seguida, calcula-se as frequências de cada tipo (equação 3), das quais se tem o tipo mais provável (equação 4). Os resultados da regularização encontram-se apresentados na Tabela 2.

Tabela 2: Resultados da regularização de litologias do furo inclinado (Tabela 1 e Fig. 1).

As coordenadas foram calculadas para o ponto médio do trecho, que representará o tipo mais provável. Aparentemente, não haveria necessidade de se fazer a transformada indicadora, pois basta ver a Tabela 1 e concluir pela litologia mais frequente.

Entretanto, quando esses mesmos dados serão utilizados para interpolação do modelo geológico, os dados só poderão ser introduzidos como funções indicadoras. Por exemplo, não faz sentido usar os tipos para calcular o tipo médio usando a equação 1, pois o resultado representado por um número decimal não terá sentido algum.

Referências:

Rivoirard, J. 1994. Introduction to disjunctive kriging and non-linear geostatistics. New York, Oxford University Press. 181p.

Yamamoto, J.K.; Rocha, M.M. 2001. Inventário e avaliação dos parâmetros geológicos e geométricos para o cálculo de reservas. In: Yamamoto, J.K. (org.) Avaliação e classificação de reservas minerais. EDUSP, São Paulo. p. 35-48.

Yamamoto, J.K.; Mao, X.M.; Koike, K.; Crosta, A.P. Landim, P.M.B.; Hu, H.Z.; Wang, C.Y.; Yao, L.Q. 2012. Mapping an uncertainty zone between interpolated types of a categorical variable. Comput. & Geosci., v. 40, p. 146-152.

Continue acompanhando os nossos posts. No próximo artigo continuaremos falando sobre Regularização.