Como calcular o número de classes de um histograma pela regra de Sturges

Em continuidade aos dois últimos artigos que trataram das distribuições normal e lognormal, neste vamos abordar como se calcula o número de classes de um histograma.

Este artigo foi derivado (com ajustes) dos itens 3.2 e 3.2.2 do Capítulo 3: Análise estatística do nosso livro: Estatística, análise e Interpolação de dados geoespaciais (Yamamoto, 2020, p. 49 e 52-53).

Distribuição de frequências

Uma lista desorganizada de números representando as realizações de experimentos não é facilmente assimilada

(Benjamin e Cornell, 1970, p. 4)

Segundo esses autores, existem vários métodos de organização, apresentação e redução de dados observados que facilitam a interpretação e avaliação.

As N observações, que foram medidas em uma amostra, podem ser classificadas em ordem crescente. Atribuindo-se frequências iguais a 1/N para cada uma delas, tem-se uma distribuição de frequências. A distribuição de frequências pode ser representada graficamente por meio da curva acumulativa (item 3.2.1 Curva acumulativa, Yamamoto, 2020, p. 50-52) ou histograma, assunto deste artigo.

Histograma

Uma representação da distribuição de frequências pode ser obtida se agrupando as frequências por intervalos ou em classes dos valores dos dados. Os intervalos ou classes são definidos dentro dos limites mínimo e máximo dos dados [xmin, xmax]. O tamanho da classe xc é obtido dividindo-se o intervalo de variação pelo número de classes:

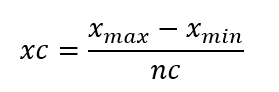
Assim, sabendo-se o número de classes, pode-se acumular as frequências 1/N em cada classe e fazer a representação gráfica como barras verticais proporcionais às frequências das classes.

Número de classes do histograma: regra de Sturges

No item anterior, o tamanho da classe foi determinado para um número de classes (nc) conhecido. Esse valor não pode ser nem tão pequeno e nem tão grande, uma vez que o objetivo é sumariar os dados disponíveis.

Dentre as fórmulas existentes para o cálculo do número de classes, sempre em função do número de pontos de dados (N), a mais efetiva e, por isso, mais popular é a Regra de Sturges (Haan, 1977, p. 17-18; Wellmer, 1998, p. 10). Segundo esses autores, o número de classes pode ser calculado, conforme:

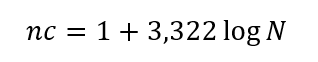
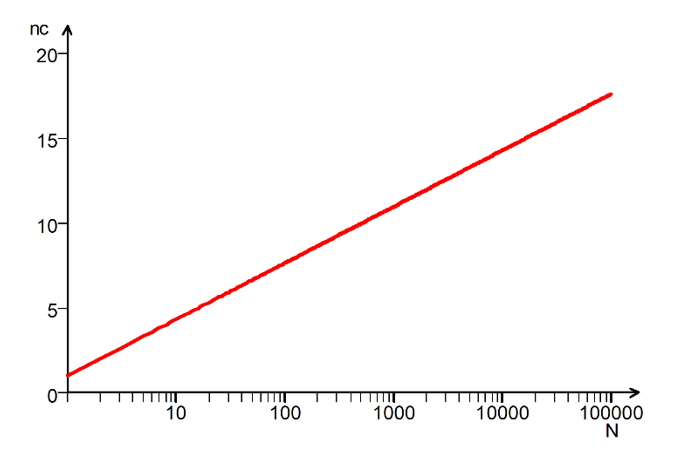
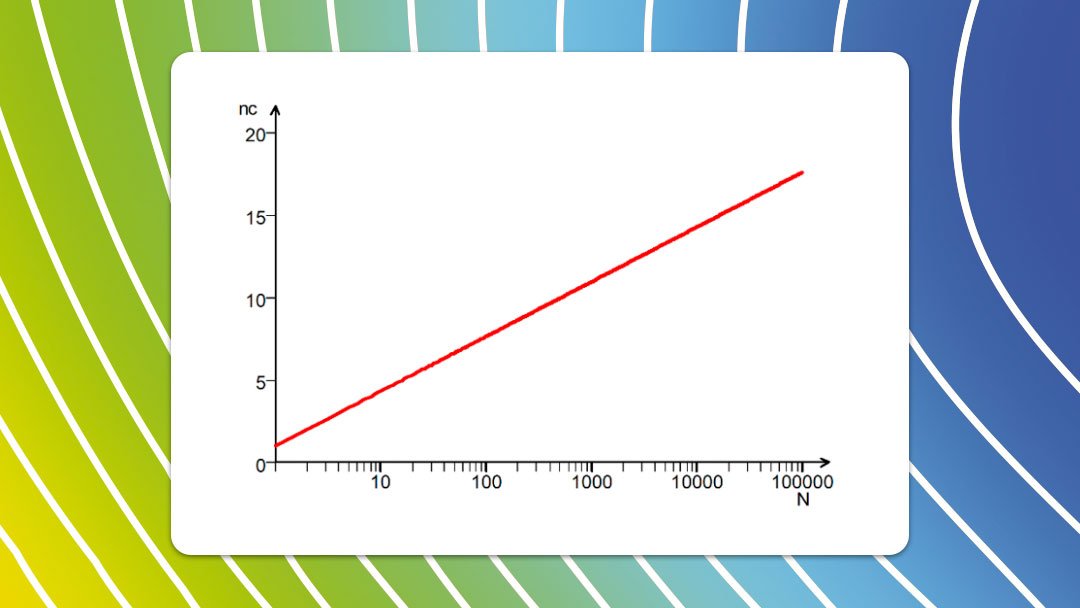
A Regra de Sturges é uma função linear em escala logarítmica, como se pode observar na Figura 1, onde o máximo para 100000 pontos de dados é 18.

Definido o número de classes, os dados são classificados acumulando-se as frequências 1/N. Assim, as frequências obtidas em cada classe são representadas como barras verticais proporcionais às frequências das classes, resultando no histograma.

Para ilustrar uma aplicação prática da regra de Sturges, seja um conjunto de dados completo com 2500 pontos (população) do qual se extrai uma amostra aleatória estratificada com 100 pontos. Assim, tem-se:

Pelos resultados obtidos, verifica-se que para a amostra com 100 pontos, o número de classes do histograma é igual a 8, enquanto para a população com 2500 pontos, o número de classes é 13. A Figura 2 representa os histogramas para a amostra e população.

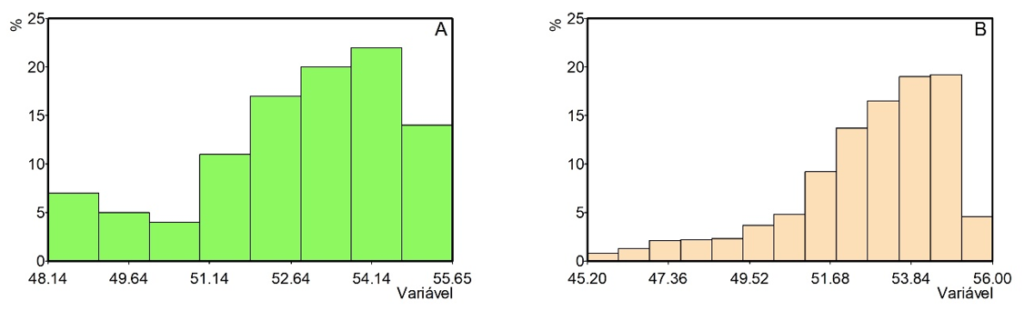
Como se trata de uma amostra com apenas 100 pontos de dados, observa-se que a amostragem não contempla os limites mínimo e máximo da população. Além disso, a cauda inferior não foi amostrada adequadamente.

Pode-se ver que há uma correlação entre os dois histogramas, mas a verificação dessa aderência é mais bem feita na forma de curvas acumulativas, como se apresenta a seguir (Figura 3).

De acordo com esta figura, confirma-se as observações feitas anteriormente, onde a cauda inferior não representa a população, da qual foi derivada. Os demais pontos da amostra estão correlacionados com a população.

Considerações finais

Este artigo apresentou a regra de Sturges para o cálculo do número de classes de um histograma.

Conforme a aplicação prática utilizada, o número de classes não aumenta linearmente com o número de pontos de dados. Por esse motivo, a regra de Sturges é melhor que outros critérios como, por exemplo, o da raiz quadrada, onde o número de classes é igual à raiz quadrado do número de dados.

Adquira o livro e tenha acesso a todo esse conteúdo exclusivo!

Referências bibliográficas

Benjamin, J.R.; Cornell, C.A. 1970. Probability, statistics and decision for civil engineers. Mineola, Dover Publications Inc. 684p.

Haan, C.T. 1977. Statistical methods in hydrology. Ames, The Iowa State University Press. 378p.

Wellmer, F.W. 1998. Statistical evaluations in exploration for mineral deposits. Heidelberg, Springer. 379p.

Yamamoto, J.K. 2020. Estatística, análise e interpolação de dados geoespaciais. São Paulo, Gráfica Paulo’s. 308p.

Próximo artigo

O próximo artigo irá apresentar a regressão robusta, que é baseada na minimização dos desvios absolutos. A regressão robusta é indicada para conjuntos de dados que apresentem pontos anômalos, devidos a erros de digitação ou erros produzidos por desvio instrumental.