Script em R do Método Iterativo de Gauss Seidel
Em continuidade ao artigo anterior, vamos apresentar o código em R para resolução de sistemas lineares pelo método iterativo de Gauss Seidel.
O ponto de partida é a seguinte equação, que permite a solução pelo processo iterativo (Venkateshan e Swaminathan, 2014, p. 87):

Onde D é a matriz diagonal, L é matriz triangular inferior e U a matriz triangular superior, decomposta a partir da matriz dos coeficientes A.
Como mencionado no artigo anterior, a cada iteração, calcula-se o vetor dos resíduos:

O erro é calculado pelo produto escalar do vetor de resíduos (2), como:

O Script GK4 resolve o sistema de equações lineares pelo método de Gauss Seidel, parcialmente baseado em código MATLAB de Venkateshan e Swaminathan (2014, p. 88-89).
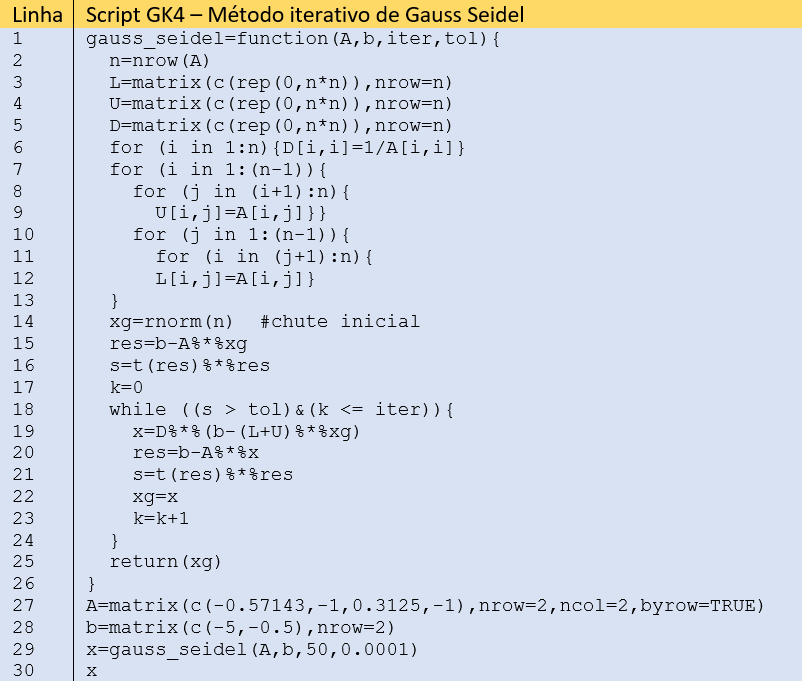
Vale comentar a facilidade da programação orientada a objetos do R, que permite converter a equação (1) em apenas uma linha de código do R (Linha 19). Pequenas modificações foram feitas no Script GK4.R de modo a permitir o desenho do gráfico da Figura 1 (Script GK5.R).

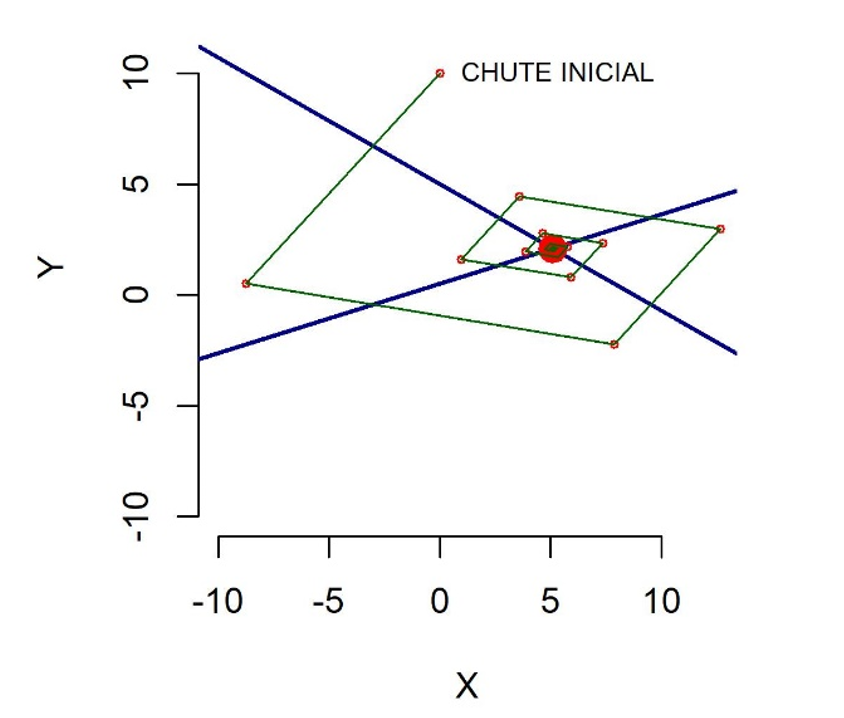
A Figura 1 ilustra o procedimento iterativo de Gauss Seidel para resolução de sistemas lineares. Como mencionado anteriormente, o Script GK4.R foi modificado para permitir o armazenamento das soluções (xRes[]), que foram usadas para desenhar o caminho percorrido pelo algoritmo para se chegar à solução esperada, dentro da tolerância especificada.
Observação importante: Este artigo foi derivado de um novo livro em preparação pelo Autor intitulado “R na prática”.
Referência Bibliográfica
Venkateshan, S.P.; Swaminathan, P. 2014. Computational methods in engineering. Waltham, Academic Press. 672p.
Próximos artigos
O próximo artigo em continuidade a este, abordará a questão da convergência do método de Gauss Seidel, em função da definição da matriz dos coeficientes como estritamente diagonal dominante. Além dos artigos em álgebra linear, deve-se postar outros na área de estatística inferencial, sobretudo abordando a programação dos testes de hipóteses. O objetivo não é simplesmente mostrar como funciona um determinado teste, mas descrever a teoria, fazer uma demonstração numérica e, em seguida, apresentar a programação em R e comparar os resultados com a função de biblioteca correspondente, visando à validação do script desenvolvido.
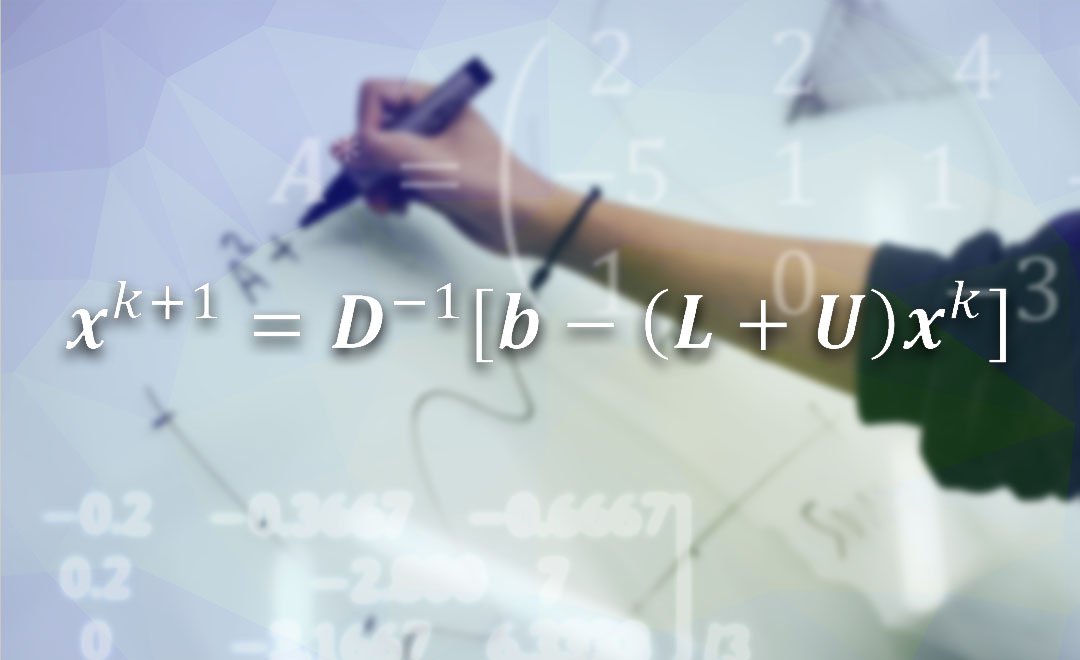
Deixe um comentário
Você precisa fazer o login para publicar um comentário.