Distribuições de probabilidades contínuas em geologia e mineração
Conforme mencionado no artigo anterior, neste, verificaremos o tipo de distribuição de probabilidades que melhor descreve a distribuição de frequências em estudo.
As estatísticas descritivas foram calculadas para uma distribuição de frequências simétrica. Assim, torna-se importante introduzir distribuições com assimetria para observar como se comportam as estatísticas descritivas.
Para isso, as duas amostras aleatórias estratificadas extraídas dos conjuntos completos positiva.txt e negativa.txt serão consideradas a seguir. As distribuições de frequências dessas amostras encontram-se nas Tabelas 2 e 3.

Tabela 2: Distribuição de frequências da variável Zlog.

Tabela 3: Distribuição de frequências da variável Zneg.
As estatísticas descritivas dessas distribuições de frequência encontram-se na Tabela 4. Conforme se observa nesta tabela, o coeficiente de variação da variável Zlog é 1,294 enquanto para a variável Zneg é apenas 0,038.
O coeficiente de variação permite verificar rapidamente o tipo de distribuição de frequências em estudo. Geralmente, coeficientes de variação maiores que 0,50 indicam distribuições de frequências com assimetria positiva. Pode-se conferir a assimetria de uma distribuição calculando-se a diferença entre a média e a mediana.
Para a variável Zlog essa diferença é 0,542, mas para a variável Zneg a diferença é negativa e igual a -0,349. Assim, conclui-se que a distribuição de Zlog apresenta assimetria positiva, enquanto Zneg tem assimetria negativa.

Tabela 4: Estatísticas descritivas para as variáveis Zgauss, Zlog e Zneg.
Distribuições de frequências com assimetrias positiva e negativa
A Figura 7 apresenta sinteticamente os resultados para as distribuições de frequências das variáveis Zlog e Zneg. As distribuições de probabilidades contínuas, representadas na figura 7, são comumente encontradas em geologia e mineração. No caso da distribuição de frequências com assimetria positiva, verifica-se apenas os momentos positivos, ao passo que aqueles momentos para valores menores que a média são tão pequenos que não são passíveis de visualização.
Nesse caso, o momento de 3ª ordem é igual a 36,039. Para a distribuição de frequências com assimetria negativa, o momento de 3ª ordem é negativo e igual a -8,410. Os coeficientes de assimetria podem ser calculados como:
![]()
Os resultados confirmam as assimetrias conforme observadas nos histogramas (Figuras 7A e 7B), bem como conforme as diferenças entre média e mediana.
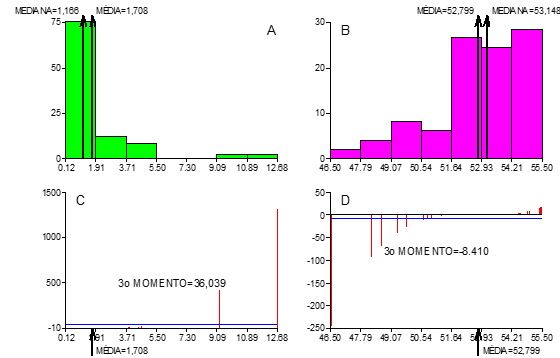
Figura 7: Distribuições de frequências com assimetria positiva (A) e com assimetria negativa (B);
momentos de 3ª ordem para distribuição com assimetria positiva (C)
e para distribuição com assimetria negativa (D).
Na natureza, teores de elementos maiores (e.g. CaCO3 em calcários) tendem a apresentar distribuições de frequências simétricas. Este tipo de distribuição é muito mais simples de se analisar, devido a simetria de valores em torno das medidas de tendência central.
Distribuições de frequências com assimetria positiva são observadas geralmente para teores de metais raros (Cu, Sn, W, Au, Ag etc.). Estas distribuições se caracterizam pela grande quantidade de valores baixos e poucos valores altos. Na estimativa de pontos ou blocos não amostrados, estes poucos teores altos tendem a contaminar os resultados. Evidentemente, isso requer a transformação dos dados, cujo objetivo principal é a mudança da forma do histograma tornando-a mais simétrica possível.
Algumas variáveis estudadas na mineração podem apresentar distribuições de frequências com assimetrias negativas. Ao contrário da assimetria positiva, este tipo de distribuição de frequências não representa dificuldades na solução de problemas de estimativa de pontos ou blocos não amostrados.
Geralmente, a dispersão é muito pequena, que pode ser confirmada pelo coeficiente de variação. A fim de ilustrar a ocorrência de teores com distribuições de frequências com assimetrias negativas, sejam dois exemplos: o teor de ferro metálico em minérios hematíticos ou magnetíticos; teor de CaO em calcários para fabricação de cimento Portland.
Considerando um minério hematítico, tem-se que a massa de uma molécula de hematita é dada por:

Assim, no caso da variável Fe metálico em minério hematítico, o valor máximo possível é 69,94%. Na realidade, este valor trunca a distribuição de frequências, tornando assimétrica negativa.
No caso de calcário, para fabricação de cimento Portland, usa-se a variável CaO. Levando em conta que o mineral de minério é a calcita, tem-se:

Para calcários, o teor máximo de CaO é igual a 56,03%, que trunca a distribuição de frequências de CaCO3, geralmente normal, transformando-a para uma distribuição com assimetria negativa.
Koch e Link (1970, p. 229-231) mencionam outras variáveis que podem apresentar distribuições de frequência com assimetria negativa: potássio em granitos; sílica em areias industriais e crômio em cromitas.
O próximo artigo irá tratar do cálculo do intervalo de confiança da média que permite determinar o intervalo no qual se encontra a média populacional a um determinado nível de confiança.
Referências:
Koch, G.S.; Link, R.F. 1970. Statistical analysis of geological data. New York, Dover Publications Inc. Vol. I. 375 p.; Vol. II. 438p.





